��Ŀ����
����Ŀ������ƽ��ֱ������ϵxOy�еĵ�P�͡�C���������¶��壺�����ڹ���P��ֱ��l����C�����ڵ�P��A��B���㣬��P��A��B�����У�λ���м�ĵ�ǡΪ����������Ϊ�˵���߶ε��е�ʱ����Ƶ�PΪ��C �����ڵ㣬ֱ��lΪ��C���ڵ�P�������ߣ�
��1������O�İ뾶Ϊ1ʱ��
�ٷֱ��ж��ڵ�D�� ![]() ��
�� ![]() ����E��0����
����E��0���� ![]() ����F��4��0���У��ǡ�O�����ڵ�����
����F��4��0���У��ǡ�O�����ڵ�����
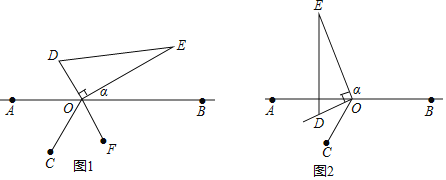
����Ӣ��еĴ��У���ѡһ�����ڵ㣬��ͼ1��������O��������һ�������ߣ���˵�������ͼ���̣�
�۵�P��ֱ��y=��x+3�ϣ�����PΪ��O�����ڵ㣬���P�������ȡֵ��Χ��
��2����C��Բ����x���ϣ��뾶Ϊ1��ֱ��y=�� ![]() ��x�ᣬy��ֱ��ڵ�M��N�����߶�MN�ϴ��ڡ�C�����ڵ�P��ֱ��д��Բ��C�ĺ������ȡֵ��Χ��
��x�ᣬy��ֱ��ڵ�M��N�����߶�MN�ϴ��ڡ�C�����ڵ�P��ֱ��д��Բ��C�ĺ������ȡֵ��Χ��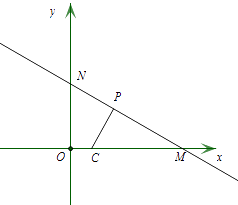
���𰸡�
��1��D��E,�⣺������OD,����D��OD�Ĵ��߽���O��A��B����,��ͼ��ʾ�� 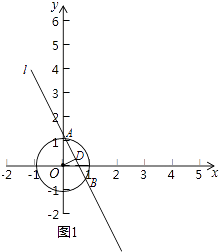 ,����x=0����y=��x+3,��y=3,��y=0����y=��x+3,��x=3,��y=��x+3��������Ľ���Ϊ��0,3���ͣ�3,0�������ڵ�P��ֱ��y=��x+3��,�ҵ�P�ǡ�O�����ڵ�,��0��PO��3,��PO��1�֡ߵ�P�ڡ�O��,��1��PO��3,��p�ĺ����귶ΧΪ��0��x��3��
,����x=0����y=��x+3,��y=3,��y=0����y=��x+3,��x=3,��y=��x+3��������Ľ���Ϊ��0,3���ͣ�3,0�������ڵ�P��ֱ��y=��x+3��,�ҵ�P�ǡ�O�����ڵ�,��0��PO��3,��PO��1�֡ߵ�P�ڡ�O��,��1��PO��3,��p�ĺ����귶ΧΪ��0��x��3��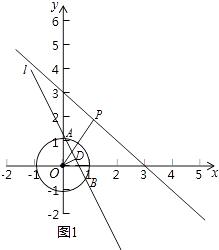
��2���⣺��x=0����y=�� ![]() x+2
x+2 ![]() ��
��
��y=2 ![]() ��
��
��N��0��2 ![]() ����
����
��y=0����y=�� ![]() x+2
x+2 ![]() ��
��
��x=6��
��M��6��0����
�ߵ�P�ǰ뾶Ϊ1�ġ�C�����ڵ㣬
��0��PC��3��PC��1��
���C���Ե�PΪԲ�ģ��뾶Ϊ3��Բ�ڣ��Ҳ������Ե�PΪԲ�ģ��뾶Ϊ1��Բ�ϣ�
�ߵ�C��x���ϣ�
���C�ĺ����귶Χ��ȡֵ��Χ��0��x��9��
���������⣺��1���ɶ����֪��
����P�ڡ�C��ʱ��
�ɴ���������֪����P��Ϊ��C�����ڵ㣬
��ʱ��0��PC��1��
����P�ڡ�C��ʱ��
���A��PB���е㣬
����PC����C�ڵ�M��
�ӳ�PC����C�ڵ�N��
����AM��BN��

�ߡ�AMP+��NMA=180�㣬
��B+��NMA=180�㣬
���AMP=��B��
�ߡ�P=��P��
���AMP�ס�NBP��
�� ![]() =
= ![]() ��
��
��PAPB=PMPN��
�ߵ�A��PB���е㣬
��AB=PA��
�֡ߡ�C�İ뾶Ϊ1��
��2AB2=��PC��CM����PC+CN����
��2AB2=PC2��1��
�֡�AB�ǡ�C���ң�
��AB��2��
��2AB2��8��
��PC2��1��8��
��PC2��9��
��PC��3��
�ߵ�P�ڡ�C�⣬
��PC��1��
��1��PC��3��
����P�ڡ�C��ʱ��
��ʱPC=1�������������⣬
�����������뾶Ϊ1�ġ�C������P��Բ��C�ľ������㣺0��PC��3����PC��1ʱ����PΪ��C�����ڵ㣻
�١�D�� ![]() ��
�� ![]() ����
����
��DO= ![]() =
= ![]() ��
��
��E��0���� ![]() ����
����
��OE= ![]() ��
��
��F��4��0����
��OF=4��
��D��E�ǡ�O�����ڵ㣻