题目内容
【题目】我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“內似线”.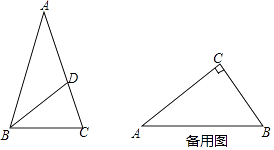
(1)等边三角形“內似线”的条数为;
(2)如图,△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求证:BD是△ABC的“內似线”;
(3)在Rt△ABC中,∠C=90°,AC=4,BC=3,E、F分别在边AC、BC上,且EF是△ABC的“內似线”,求EF的长.
【答案】
(1)3
(2)证明:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD,
∴△BCD∽△ABC,
又∵∠BDC=∠A+∠ABD,
∴∠ABD=∠CBD,
∴BD平分∠ABC,
即BD过△ABC的内心,
∴BD是△ABC的“內似线”;
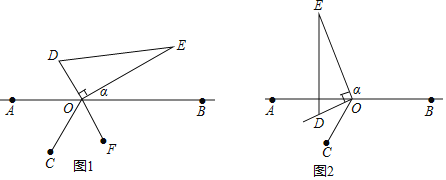
(3)解:设D是△ABC的内心,连接CD,
则CD平分∠ACB,
∵EF是△ABC的“內似线”,
∴△CEF与△ABC相似;
分两种情况:①当 ![]() =
= ![]() =
= ![]() 时,EF∥AB,
时,EF∥AB,
∵∠ACB=90°,AC=4,BC=3,
∴AB= ![]() =5,
=5,
作DN⊥BC于N,如图2所示:
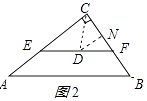
则DN∥AC,DN是Rt△ABC的内切圆半径,
∴DN= ![]() (AC+BC﹣AB)=1,
(AC+BC﹣AB)=1,
∵CD平分∠ACB,
∴ ![]() =
= ![]() ,
,
∵DN∥AC,
∴ ![]() =
= ![]() ,即
,即 ![]() ,
,
∴CE= ![]() ,
,
∵EF∥AB,
∴△CEF∽△CAB,
∴ ![]() ,即
,即 ![]() ,
,
解得:EF= ![]() ;
;
②当 ![]() =
= ![]() =
= ![]() 时,同理得:EF=
时,同理得:EF= ![]() ;
;
综上所述,EF的长为 ![]() .
.
【解析】(1)解:等边三角形“內似线”的条数为3条;理由如下:
过等边三角形的内心分别作三边的平行线,如图1所示:
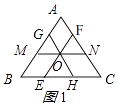
则△AMN∽△ABC,△CEF∽△CBA,△BGH∽△BAC,
∴MN、EF、GH是等边三角形ABC的內似线”;
所以答案是:3.
【考点精析】本题主要考查了相似三角形的应用的相关知识点,需要掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能正确解答此题.

 每课必练系列答案
每课必练系列答案