题目内容
【题目】如图,抛物线y=﹣ ![]() x2+
x2+ ![]() x+2与x轴交于点A,B,与y轴交于点C.
x+2与x轴交于点A,B,与y轴交于点C.
(1)试求A,B,C的坐标;
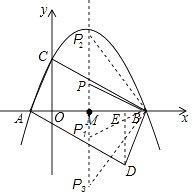
(2)将△ABC绕AB中点M旋转180°,得到△BAD.
①求点D的坐标;
②判断四边形ADBC的形状,并说明理由;
(3)在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请直接写出所有满足条件的P点的坐标;若不存在,请说明理由.
【答案】
(1)
解:当y=0时,0=﹣ ![]() x2+
x2+ ![]() x+2,
x+2,
解得:x1=﹣1,x2=4,
则A(﹣1,0),B(4,0),
当x=0时,y=2,
故C(0,2)
(2)
解:①过点D作DE⊥x轴于点E,
∵将△ABC绕AB中点M旋转180°,得到△BAD,
∴DE=2,AO=BE=1,OM=ME=1.5,
∴D(3,﹣2);
②∵将△ABC绕AB中点M旋转180°,得到△BAD,
∴AC=BD,AD=BC,
∴四边形ADBC是平行四边形,
∵AC= ![]() =
= ![]() ,BC=
,BC= ![]() =2
=2 ![]() ,
,
AB=5,
∴AC2+BC2=AB2,
∴△ACB是直角三角形,
∴∠ACB=90°,
∴四边形ADBC是矩形
(3)
解:由题意可得:BD= ![]() ,AD=2
,AD=2 ![]() ,
,
则 ![]() =
= ![]() ,
,
当△BMP∽△ADB时,
![]() =
= ![]() =
= ![]() ,
,
可得:BM=2.5,
则PM=1.25,
故P(1.5,1.25),
当△BMP1∽△ABD时,
P1(1.5,﹣1.25),
当△BMP2∽△BDA时,
可得:P2(1.5,5),
当△BMP3∽△BDA时,
可得:P3(1.5,﹣5),
综上所述:点P的坐标为:(1.5,1.25),(1.5,﹣1.25),(1.5,5),(1.5,﹣5)
【解析】(1)直接利用y=0,x=0分别得出A,B,C的坐标;(2)①利用旋转的性质结合三角形各边长得出D点坐标;②利用平行四边形的判定方法结合勾股定理的逆定理得出四边形ADBC的形状;(3)直接利用相似三角形的判定与性质结合三角形各边长进而得出答案.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 阅读快车系列答案
阅读快车系列答案【题目】某工厂投入生产一种机器的总成本为2000万元.当该机器生产数量至少为10台,但不超过70台时,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如下表:
x(单位:台) | 10 | 20 | 30 |
y(单位:万元∕台) | 60 | 55 | 50 |
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求该机器的生产数量;
(3)市场调查发现,这种机器每月销售量z(台)与售价a(万元∕台)之间满足如图所示的函数关系.该厂生产这种机器后第一个月按同一售价共卖出这种机器25台,请你求出该厂第一个月销售这种机器的利润.(注:利润=售价﹣成本) 


