题目内容
【题目】如图1是一个长为2a,宽为2b的 长方形,沿图中虚线剪开分成四块小长方形,然后按如图2的形状拼成一个正方形。
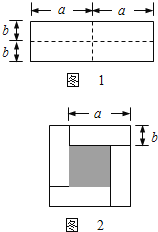
(1)图2的阴影部分的正方形的边长是 .
(2)用两种不同的方法求图中阴影部分的面积.
(方法1)S阴影= ;
(方法2)S阴影= ;
(3)观察如图2,写出(a+b)2、(a-b)2,ab三个代数式之间的等量关系.
(4)根据(3)题中的等量关系,解决问题:若x+y=10,xy=16,求x-y的值。
【答案】(1)a-b;(2)(a+b)2-4ab,(a-b)2;(3)(a+b)2-4ab=(a-b)2;(4)±6
【解析】
(1)观察图意直接得出正方形的边长是a-b;(2)利用大正方形的面积减去4个小长方形的面积,或者直接利用(1)的条件求出小正方形的面积;(3)把(2)中的两个代数式联立即可;(4)类比(3)求出(x-y)2,再开方即可.
(1)观察图意直接得出正方形的边长是a-b;
(2)利用大正方形的面积减去4个小长方形的面积则S阴影=(a+b)2-4ab,
直接利用(1)的条件求出小正方形的面积则S阴影=(a-b)2;
(3)由S阴影的两种写法得(a+b)2-4ab=(a-b)2;
(4)由(3)可得(x-y)2=(x+y)2-4xy,
则(x-y)2=102-4×16=36,
∴x-y=±6,

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
【题目】观察图形,解答问题:

(1)按下表已填写的形式填写表中的空格:
图① | 图② | 图③ | |
三个角上三个数的积 | 1×(﹣1)×2=﹣2 | (﹣3)×(﹣4)×(﹣5)=﹣60 |
|
三个角上三个数的和 | 1+(﹣1)+2=2 | (﹣3)+(﹣4)+(﹣5)=﹣12 |
|
积与和的商 | (﹣2)÷2=﹣1 |
|
|
(2)请用你发现的规律求出图④中的数x.