题目内容
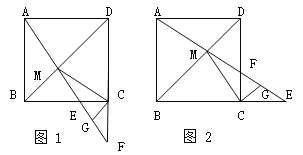
【题目】两组邻边分别相等的四边形我们称它为筝形,如图,在筝形ABCD中,AB=AD,BC=DC,AC,BD相交于点O.

(1)求证:①△ABC≌△ADC;②OB=OD,AC⊥BD;
(2)如果AC=6,BD=4,求筝形ABCD的面积.
【答案】(1)见解析;(2)12;
【解析】
(1)分别利用SSS,SAS求证△ABC≌△ADC,△ABO≌△ADO,从而得出OB=OD,AC⊥BD.
(2)筝形的面积公式可用△ABC的面积与△ACD的面积和求得.
(1)证明:①在△ABC和△ADC中,
AB=AD,BC=DC,AC=AC,
∴△ABC≌△ADC(SSS).
②∵△ABC≌△ADC,
∴∠BAO=∠DAO.
∵AB=AD,∠BAO=∠DAO,OA=OA,
∴△ABO≌△ADO(SAS).
∴OB=OD,AC⊥BD.
(2)筝形ABCD的面积=△ABC的面积+△ACD的面积=![]() ×AC×BO+
×AC×BO+![]() ×AC×DO=
×AC×DO=![]() ×AC×(BO+DO)=
×AC×(BO+DO)=![]() ×AC×BD=
×AC×BD=![]() ×6×4=12.
×6×4=12.

练习册系列答案
相关题目