题目内容
【题目】(1)如图,在四边形 ![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求证:
,求证:![]() .
.

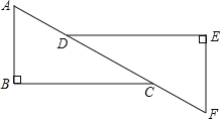
(2)如图,在离水面高度为 ![]() 米的岸上,有人用绳子拉船靠岸,开始时绳子
米的岸上,有人用绳子拉船靠岸,开始时绳子 ![]() 的长为
的长为 ![]() 米,此人以
米,此人以 ![]() 米每秒的速度收绳,
米每秒的速度收绳,![]() 秒后船移动到点
秒后船移动到点 ![]() 的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号).
的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号).

【答案】(1)见详解.
(2)![]()
【解析】
(1)先根据勾股定理求出BD的长度,然后根据勾股定理的逆定理,即可证明AD⊥BD;
(2)
开始时,AC=5,BC=13,即可求得AB的值,6秒后根据BC,AC长度即可求得AB的值,即可解题.
解:(1)∵∠C=90°,BC=4,CD=3,
∴BD=5.
又∵AB=13,AD=12,
∴![]()
即:![]() .
.
∴AD⊥BD.
(2)
解:∵在Rt△ABC中,∠CAB=90°,BC=13m,AC=5m,
∴![]() (m)
(m)
∵此人以0.5m/s的速度收绳,6s后船移动到点D的位置,
∴CD=13-0.5×6=10(m),
∴![]()
∴![]()

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
【题目】光明中学组织全校1000名学生进行了校园安全知识竞赛.为了解本次知识竞赛的成绩分布情况,从中随机抽取了部分学生的成绩(得分取正整数,满分为100分),并绘制了如图的频数分布表和频数分布直方图(不完整).
分组 | 频数 | 频率 |
50.5~60.5 | 10 | a |
60.5~70.5 | b | |
70.5~80.5 | 0.2 | |
80.5~90.5 | 52 | 0.26 |
90.5~100.5 | 0.37 | |
合计 | c | 1 |
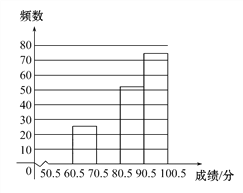
请根据以上提供的信息,解答下列问题:
(1)直接写出频数分布表中a,b,c的值,补全频数分布直方图.
(2)上述学生成绩的中位数落在哪一组范围内?
(3)学校将对成绩在90.5~100.5分之间的学生进行奖励,请估计全校1000名学生中约有多少名获奖?