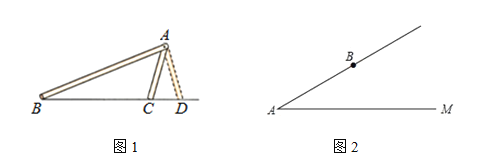题目内容
【题目】(问题情境)学习《探索全等三角形条件》后,老师提出了如下问题:如图①,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围。同学通过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,连接BE.根据SAS可证得到△ADC≌△EDB,从而根据“三角形的三边关系”可求得AD的取值范围是 。解后反思:题目中出现“中点”“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
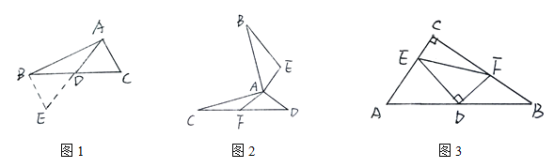
(直接运用)如图②,AB⊥AC,AD⊥AE,AB=AC,AD=AE,AF是ACD的边CD上中线.求证:BE=2AF.
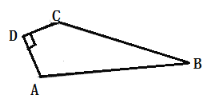
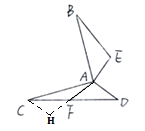
(灵活运用)如图③,在△ABC中,∠C=90°,D为AB的中点,DE⊥DF,DE交AC于点E,DF交AB于点F,连接EF,试判断以线段AE、BF、EF为边的三角形形状,并证明你的结论.
【答案】(1)2<AD<10;(2)见解析(3)为直角三角形,理由见解析.
【解析】
(1)根据△ADC≌△EDB,得到BE=AC=8,再根据三角形的构成三角形得到AE的取值,再根据D为AE中点得到AD的取值;
(2)延长AF到H,使AF=HF,故△ADF≌△HCF,AH=2AF,由AB⊥AC,AD⊥AE,得到∠BAE+∠CAD=180°,又∠ACH+∠CAH+∠AHC=180°,根据∠D=∠FCH,∠DAF=∠CHF,得到∠ACH+∠CAD=180°,故∠BAE= ACH,再根据AB=AC,AD=AE即可利用SAS证明△BAE≌△ACH,故BE=AH,故可证明BE=2AF.
(3)延长FD到点G,使DG=FD,连结GA,GE,证明△DBF≌△DAG,故得到FD=GD,BF=AG,由DE⊥DF,得到EF=EG,再求出∠EAG=90°,利用勾股定理即可求解.
(1)∵△ADC≌△EDB,
∴BE=AC=8,
∵AB=12,
∴12-8<AE<12+8,
即4<AE<20,
∵D为AE中点
∴2<AD<10;
(2)延长AF到H,使AF=HF,
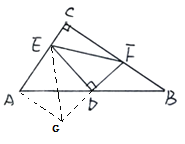
由题意得△ADF≌△HCF,故AH=2AF,
∵AB⊥AC,AD⊥AE,
∴∠BAE+∠CAD=180°,
又∠ACH+∠CAH+∠AHC=180°,
∵∠D=∠FCH,∠DAF=∠CHF,
∴∠ACH+∠CAD=180°,
故∠BAE= ACH,
又AB=AC,AD=AE
∴△BAE≌△ACH(SAS),
故BE=AH,又AH=2AF
∴BE= 2AF.
(3)以线段AE、BF、EF为边的三角形为直角三角形,理由如下:
延长FD到点G,使DG=FD,连结GA,GE,
由题意得△DBF≌△ADG,
∴FD=GD,BF=AG,
∵DE⊥DF,
∴DE垂直平分GF,
∴EF=EG,
∵∠C=90°,
∴∠B+∠CAB=90°,
又∠B=∠DAG,
∴∠DAG +∠CAB=90°
∴∠EAG=90°,
故EG2=AE2+AG2,
∵EF=EG, BF=AG
∴EF2=AE2+BF2,
则以线段AE、BF、EF为边的三角形为直角三角形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案