题目内容
【题目】如图，在△ABC中, ∠C = 90°，∠B= 30°，点D是线段AB的垂直平分线与BC的交点， 连接AD,则△ACD与△ADB的面积比为（ ）
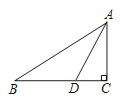
A.1B.
C.
D.
【答案】B
【解析】
根据垂直平分线的性质可得AD=BD，∠DAB=∠B=30°，进一步可求出∠CAD的度数，根据直角三角形中30°的角所对的直角边等于斜边的一半，求出CD与BD的关系，即可求解.
∵∠C = 90°，∠B= 30°
∴∠CAB=60°
∵点D是线段AB的垂直平分线与BC的交点
∴AD=BD，∠DAB=∠B=30°，
∴∠CAD=30°
∴CD=
AD=BD
∴CD∶BD=1∶2
△ACD的面积=AC×CD；△ABD的面积=AC×BD
∴△ACD与△ADB的面积比为
故选：B
练习册系列答案
相关题目
【题目】甲、乙两名学生进行射击练习，两人在相同条件下各射靶10次，将射击结果作统计分析如下：
命中环数 | 5 | 6 | 7 | 8 | 9 | 10 |
甲命中环数的次数 | 1 | 4 | 2 | 1 | 1 | 1 |
乙命中环数的次数 | 1 | 2 | 4 | 2 | 1 | 0 |
请你从射击稳定性方面评价甲、乙两人的射击水平，则_____比较稳定（填“甲”或“乙”）．
【题目】某超市计划购进甲、乙两种商品，两种商品的进价、售价如下表：
商品 | 甲 | 乙 |
进价（元/件） |
|
|
售价（元/件） | 200 | 100 |
若用360元购进甲种商品的件数与用180元购进乙种商品的件数相同．
（1）求甲、乙两种商品的进价是多少元？
（2）若超市销售甲、乙两种商品共50件，其中销售甲种商品为
件（
），设销售完50件甲、乙两种商品的总利润为
元，求与之间的函数关系式，并求出的最小值．
