题目内容
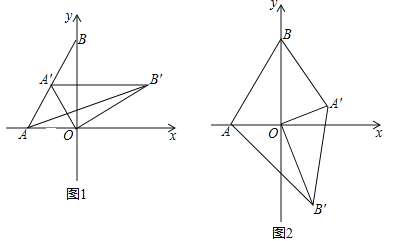
【题目】如图1,在平面直角坐标系中,将![]() 放置在第一象限,且
放置在第一象限,且![]() 轴,直线
轴,直线![]() 从原点出发沿
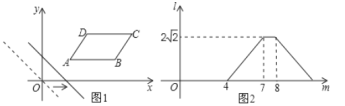
从原点出发沿![]() 轴正方向平移,在平移过程中直线被平行四边形截得的线段长度
轴正方向平移,在平移过程中直线被平行四边形截得的线段长度![]() 与直线在
与直线在![]() 轴上平移的距离
轴上平移的距离![]() 的函数图象如图2所示,则平行四边形
的函数图象如图2所示,则平行四边形![]() 的面积为___________.
的面积为___________.
【答案】8
【解析】
根据图象可以得到当移动的距离是4时,直线经过点![]() ,当移动距离是7时,直线经过
,当移动距离是7时,直线经过![]() ,在移动距离是8时经过
,在移动距离是8时经过![]() ,则
,则![]() ,当直线经过
,当直线经过![]() 点,设交
点,设交![]() 与
与![]() ,则
,则![]() ,作
,作![]() 于点
于点![]() .利用三角函数即可求得
.利用三角函数即可求得![]() 即平行四边形的高,然后利用平行四边形的面积公式即可求解.
即平行四边形的高,然后利用平行四边形的面积公式即可求解.
解:根据图象可以得到当移动的距离是4时,直线经过点![]() ,当移动距离是7时,直线经过
,当移动距离是7时,直线经过![]() ,在移动距离是8时经过
,在移动距离是8时经过![]() ,
,
则![]() ,
,
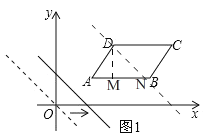
如图,当直线经过![]() 点,设交
点,设交![]() 与
与![]() ,
,
∵由图像得直线![]() 在从N到B的移动过程中DN长不变,
在从N到B的移动过程中DN长不变,
∴![]() .
.
作![]() 于点
于点![]() .
.
![]() 与
与![]() 轴形成的角是
轴形成的角是![]() ,
,
又![]() 轴,
轴,
![]() ,
,
![]() ,
,
则平行四边形的面积是:![]() .
.
故答案为:8.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
【题目】某礼品店从文化用品市场批发甲、乙、丙三种礼品(每种礼品都有),各礼品的数量和批发单价列表如下:
甲 | 乙 | 丙 | |
数量(个) |
|
|
|
批发单价(元) |
|
|
|
|
![]() 当
当![]() 时,若这三种礼品共批发
时,若这三种礼品共批发![]() 个,甲礼品的总价不低于丙礼品的总价,求
个,甲礼品的总价不低于丙礼品的总价,求![]() 的最小值.
的最小值.
![]() 已知该店用
已知该店用![]() 元批发了这三种礼品,且
元批发了这三种礼品,且![]() .
.
![]() 当
当![]() 时,若批发这三种礼品的平均单价为
时,若批发这三种礼品的平均单价为![]() 元/个,求
元/个,求![]() 的值.
的值.
![]() 当
当![]() 时,若该店批发了
时,若该店批发了![]() 个丙礼品,且
个丙礼品,且![]() 为正整数,求
为正整数,求![]() 的值.
的值.