题目内容
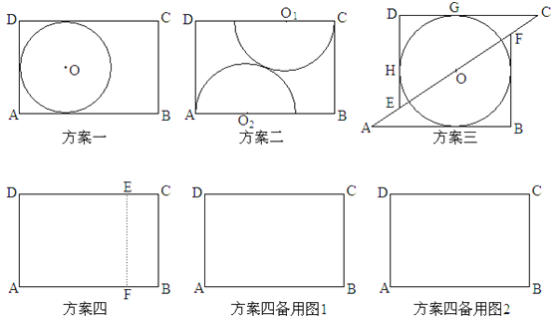
【题目】木匠黄师傅用长AB=3,宽BC=2的矩形木板做一个尽可能大的圆形桌面,他设计了四种方案:
方案一:直接锯一个半径最大的圆;
方案二:圆心O1,O2分别在CD,AB上,半径分别是O1C,O2A,锯两个外切的半圆拼成一个圆;
方案三:沿对角线AC将矩形锯成两个三角形,适当平移三角形并锯一个最大的圆;
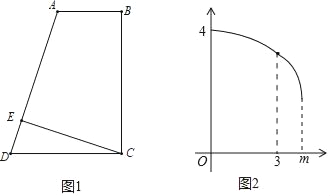
方案四:锯一块小矩形BCEF拼接到矩形AEFD下面,并利用拼成的木板锯一个尽可能大的圆。
(1)写出方案一中的圆的半径;
(2)通过计算说明方案二和方案三中,哪个圆的半径较大?
(3)在方案四中,设CE=![]() (
(![]() ),圆的半径为
),圆的半径为![]() ,
,
①求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
②当![]() 取何值时圆的半径最大?最大半径是多少?并说明四种方案中,哪一个圆形桌面的半径最大?
取何值时圆的半径最大?最大半径是多少?并说明四种方案中,哪一个圆形桌面的半径最大?
【答案】(1)方案一中圆的半径为1
(2)方案三的圆半径较大
(3) ①当0<x<时,y=![]()
当![]() 时,
时,![]()
②当![]() 时,y最大,y最大=,
时,y最大,y最大=,
四种方案中,第四种方案圆形桌面的半径最大。
【解析】
试题(1)圆的直径就是BC的长
方案二:连O1O2,作EO1⊥AB于E,然后利用勾股定理即可得
方案三:连OG,然后利用△OCG∽△CDE即可得
(3)分情况讨论:分0<x<与![]() 这两种情况进行分析
这两种情况进行分析
试题解析:(1)方案一中圆的半径为1
(2)方案二
如图,连O1O2,作EO1⊥AB于E,设O1E=X,
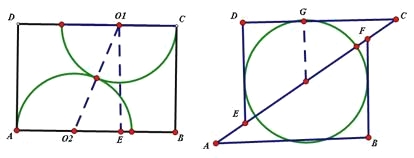
那么(2X)2=22+(3-2X)2,解得X=![]()
方案三
连OG,∴OG⊥CD,∵∠D=90°,∴OG//DE
∴△OCG∽△CDE,∴![]()
设OG=y,∴![]() ,∴y=,∴方案三的圆半径较大
,∴y=,∴方案三的圆半径较大
(3) ①当0<x<时,y=![]()
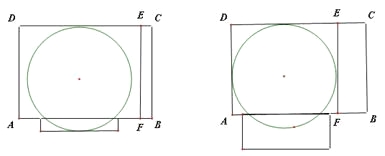
当![]() 时,
时,![]()
②当![]() 时,y最大,y最大=,
时,y最大,y最大=,
四种方案中,第四种方案圆形桌面的半径最大。

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目