题目内容
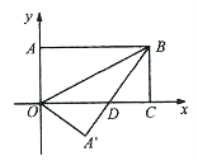
【题目】如图,把长方形纸片OABC放入平面直角坐标系中,使OC、OA分别与x轴,y轴重合,连接OB,将长方形纸片OABC沿OB折叠,使点A落在点A,的位置,A,B与x轴交于D,若点B的坐标为(4,2),则点A,的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
根据折叠性质,设OD=x,在Rt△BDC中勾股定理,得A,D=1.5,OA,=AO=2, 由△OA,D面积可得:A,E![]() DO=OA,
DO=OA,![]() A,D,求出A,E和OE的长度即可表示出坐标.
A,D,求出A,E和OE的长度即可表示出坐标.
解:过点A,向坐标轴做垂线,交点为E,F如下图,
由题可知:∠ABO=∠OBA,
∵AB∥CO,
∴∠ABO=∠BOC,
∴∠DOB=∠OBA,,
∴DO=BD,
∵B(4,2),
∴CO=4,BC=2,
设OD=x,则BD=x,DC=4-x,
在Rt△BDC中,BD2=CD2+BC2,即x2=(4-x)2+22,
解得:x=2.5,
∴A,D=4-2.5=1.5,OA,=AO=2,
由△OA,D面积可得:A,E![]() DO=OA,
DO=OA,![]() A,D,
A,D,
∴A,E=![]() =
=![]() ,
,
∴OE=![]() =
=![]() ,
,
∴A,的坐标为:![]()
故选D.

练习册系列答案
相关题目