题目内容
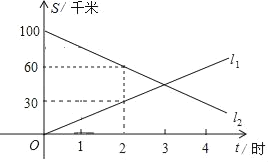
【题目】A,B两地相距100千米,甲,乙两人骑车同时分别从A、B两地相向而行,假设他们都保持匀速行驶,直线l1,l2分别表示甲,乙两人与A地的距离S(单位:km)与行驶时间t(单位:h)之间关系的图象.
根据图象提供的信息,解答下列问题:
(1)甲、乙两人的速度分别是多少?
(2)经过多长时间,两人相遇?
(3)分别写出甲,乙两人与A地的距离S(单位:km)与行驶时间t(单位:h)之间的关系式.
【答案】(1)甲的速度为: 15(km/h),乙的速度为: 20(km/h);(2)经过![]() 小时,两人相遇;(3)甲: s1=15t;乙:s2=﹣20t+100.
小时,两人相遇;(3)甲: s1=15t;乙:s2=﹣20t+100.
【解析】
(1)利用图象上点的坐标得出甲、乙的速度即可;
(2)利用待定系数法求出直线l1、l2的解析式,利用两函数相等进而求出相遇的时间;
(3)由(2)可得结论
解:(1)如图所示:甲的速度为:30÷2=15(km/h),
乙的速度为:(100﹣60)÷2=20(km/h);
(2)设l1的关系式为:s1=kt,则30=k×2,解得:k=15,故s1=15t;
设s2=at+b,将(0,100),(2,60),
则![]() ,解得:
,解得:![]() ,
,
故l2的关系式为s2=﹣20t+100;
15t=﹣20t+100,
t=![]() ,
,
答:经过![]() 小时,两人相遇;
小时,两人相遇;
(3)由(2)可知:
甲:l1的关系式为:s1=15t;
乙:l2的关系式为:s2=﹣20t+100.

【题目】已知,在一个盒子里有红球和白球共10个,它们除颜色外都相同,将它们充分摇匀后,从中随机抽出一个,记下颜色后放回.在摸球活动中得到如下数据:
摸球总次数 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
摸到红球的频数 | 17 | 32 | 44 | 64 | 78 |
| 103 | 122 | 136 | 148 |
摸到红球的频率 | 0.34 | 0.32 | 0.293 | 0.32 | 0.312 | 0.32 | 0.294 |
| 0.302 |
|
(1)请将表格中的数据补齐;
(2)根据上表,完成折线统计图;
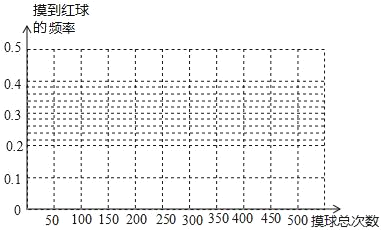
(3)请你估计,当摸球次数很大时,摸到红球的频率将会接近 (精确到0.1).