题目内容
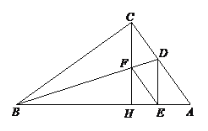
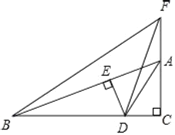
【题目】已知∠ACB=90°,AD平分∠BAC交BC于D,DE⊥AB于E,BE=AE+AF,连结BF,判断△BDF的形状,并说明理由.
【答案】△BDF是等腰三角形,理由见解析
【解析】
根据角平分线的性质得出DC=DE,再根据全等三角形的判定得出△ACD≌△AED,可得AE=AC,由BE=AE+AF可得出BE=CF,再证明△FCD≌△BED,进而得出BD=FD,则结论得证.
解:△BDF是等腰三角形,理由如下:
∵AD平分∠BAC交BC于D,DE⊥AB于E,∠ACB=90°,
∴DC=DE,
在Rt△ACD和Rt△AED中,
![]() ,
,
∴Rt△ACD≌Rt△AED(HL),
∴AE=AC,
∵BE=AE+AF,
∴BE=AC+AF=CF,
在Rt△FCD和Rt△BED中,
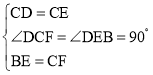 ,
,
∴Rt△FCD≌Rt△BED(SAS),
∴BD=FD,
即△BDF是等腰三角形.

练习册系列答案
相关题目