题目内容
【题目】(提高题) 如图所示,△ABC中,∠ACB=90°,∠ABC的平分线BD交AC于点D,CH⊥AB于H,且交BD于点F,DE⊥AB于E,四边形CDEF是菱形吗?请说明理由.
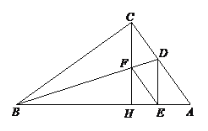
【答案】是菱形,理由见解析
【解析】
利用“有一组邻边相等的平行四边形是菱形”证明四边形CDEF是菱形即可.根据角平分线的性质先证明CD=DE,再证明四边形CDEF为平行四边形.
∵AC⊥BC,CH⊥AB;
∴∠ABC+∠6=90°, ∠ABC+∠A=90°,
∴∠A=∠6;
又∵BD平分∠ABC,
∴∠1=∠2;
又∵DE⊥AB,CD⊥BC,
∴DE=CD;
∵∠5=∠1+∠6,∠4=∠2+∠A;
∴∠5=∠4,
∴CF=CD,
∴CF=DE.
∵CH⊥AB,DE⊥AB,
∴CF∥DE,
∴四边形CDEF为平行四边形.
又∵CD=DE,
∴平行四边形CDEF为菱形.

练习册系列答案
相关题目