题目内容
若一个四边形的四个内角度数之比为1：3：4：2，则这四个内角的度数分别是______。
【答案】
36°，108°，144°，72°
【解析】
试题分析：设四边形4个内角的度数分别是x，3x，4x，2x，根据四边形的内角和定理列方程求解．
设四边形4个内角的度数分别是x，3x，4x，2x．
∴x+3x+4x+2x=360°，
解得x=36°．
所以这个四边形四个内角的度数分别为36°，108°，144°，72°．
考点：本题主要考查了多边形的内角和
点评：解答本题的关键是记住多边形内角和公式为（n-2）×180°.
练习册系列答案
阅读快车系列答案
相关题目
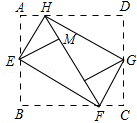如图，将矩形纸ABCD的四个角向内折起，恰好拼成一个无缝隙无重叠的四边形EFGH，若EH=3厘米，EF=4厘米，则边AD的长是
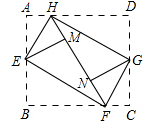如图，将矩形ABCD的四个角向内折起，恰好拼成一个既无缝隙又无重叠的四边形EFGH，若EH=3，EF=4，那么线段AD与AB的比等于
18、如图，将矩形ABCD的四个角向内折起，恰好拼成一个无缝隙又无重叠的四边形EFGH，若EH=6，EF=8．那么矩形ABCD的周长是
（2013•历城区二模）如图，将矩形ABCD的四个角向内折起，恰好拼成一个无缝隙无重叠的四边形EFGH，若AB=6厘米，∠EFH=30°，则边AD的长是
如图，将矩形纸片ABCD的四个角向内折起，恰好拼成一个既无缝隙又无重叠的四边形EFGH，若EH=3，EF=5，则矩形ABCD的面积是