题目内容
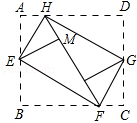 如图,将矩形纸ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3厘米,EF=4厘米,则边AD的长是
如图,将矩形纸ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3厘米,EF=4厘米,则边AD的长是分析:利用三个角是直角的四边形是矩形易证四边形EFGH为矩形,那么由折叠可得HF的长即为边AD的长.
解答:解:∵∠HEM=∠AEH,∠BEF=∠FEM,
∴∠HEF=∠HEM+∠FEM=
×180°=90°,
同理可得:∠EHG=∠HGF=∠EFG=90°,
∴四边形EFGH为矩形.
∵AD=AH+HD=HM+MF=HF,HF=
=
=5,
∴AD=5厘米.
故答案为5.
∴∠HEF=∠HEM+∠FEM=
| 1 |
| 2 |
同理可得:∠EHG=∠HGF=∠EFG=90°,
∴四边形EFGH为矩形.
∵AD=AH+HD=HM+MF=HF,HF=
| EH2+EF2 |
| 32+42 |
∴AD=5厘米.
故答案为5.
点评:主要考查学生对翻转、折叠矩形、三角形等知识的掌握情况.错误的主要原因是空间观念以及转化的能力不强,缺乏简单的逻辑推理能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
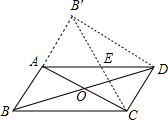 到△AB′C.
到△AB′C.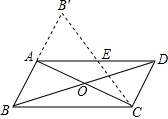 180°,得到△AB′C.
180°,得到△AB′C.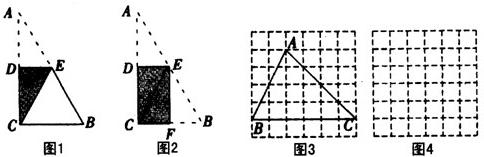
 为顶点的四边形是矩形;
为顶点的四边形是矩形;