题目内容
【题目】如图1，在平面直角坐标系中，A（0，1），B（4，1），C为x轴正半轴上一点，且AC平分∠OAB．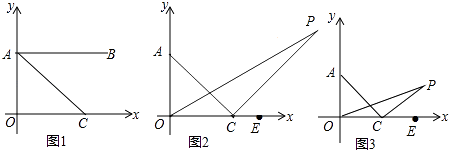 
（1）求证：∠OAC=∠OCA；
（2）如图2，若分别作∠AOC的三等分线及∠OCA的外角的三等分线交于点P，即满足∠POC= 
∠AOC，∠PCE= ∠ACE，求∠P的大小；
（3）如图3，在（2）中，若射线OP、OC满足∠POC= 
∠AOC，∠PCE= ∠ACE，猜想∠OPC的大小，并证明你的结论（用含n的式子表示）
【答案】
（1）解：∵A（0，1），B（4，1），
∴AB∥CO，
∴∠OAB=90°，
∵AC平分∠OAB．
∴∠OAC=45°，
∴∠OCA=90°﹣45°=45°，
∴∠OAC=∠OCA；
（2）解：∵∠POC= 
∠AOC，∴∠POC= ×90°=30°，
∵∠PCE= ∠ACE，∴∠PCE= （180°﹣45°）=45°，
∵∠P+∠POC=∠PCE，
∴∠P=∠PCE﹣∠POC=15°
（3）解：∵∠POC= 
∠AOC，∴∠POC= ×90°= 
°，
∵∠PCE= ∠ACE，∴∠PCE= （180°﹣45°）= 
°，
∵∠P+∠POC=∠PCE，
∴∠P=∠PCE﹣∠POC= 
°
【解析】（1）根据AB坐标可以求得∠OAB大小，根据角平分线性质可求得∠OAC大小，即可解题；（2）根据题干中给出的∠POC= ∠AOC、∠PCE= ∠ACE可以求得∠PCE和∠POC的大小，再根据三角形外角等于不相邻两内角和即可解题；（3）解法和（2）相同，根据题干中给出的∠POC= ∠AOC、∠PCE= ∠ACE可以求得∠PCE和∠POC的大小，再根据三角形外角等于不相邻两内角和即可解题．
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识，掌握由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质，以及对三角形的内角和外角的理解，了解三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角．
