如图.D为AC上一点.E是BC延长线上一点.连接BD.DE.求证:∠ADB＞∠CDE．题目和参考答案——青夏教育精英家教网—

题目内容

9．

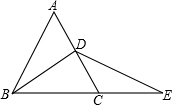如图，D为AC上一点，E是BC延长线上一点，连接BD，DE，求证：∠ADB＞∠CDE．

分析根据三角形的一个外角大于和它不相邻的任何一个内角证明即可．

解答证明：∵∠ADB是△BDC的外角，
∴∠ADB＞∠BCD，
∵∠BCD是△DCE的外角，
∴∠BCD＞∠CDE，
∴∠ADB＞∠CDE．

点评本题考查的是三角形的外角的性质，掌握三角形的一个外角大于和它不相邻的任何一个内角是解题的关键．

涓€棰樹竴棰樻壘绛旀瑙ｆ瀽澶參浜�
涓嬭浇浣滀笟绮剧伒鐩存帴鏌ョ湅鏁翠功绛旀瑙ｆ瀽绔嬪嵆涓嬭浇

练习册系列答案

相关题目

19．下列函数中，满足y的值随x的值增大而增大的是（　　）

$\sqrt{2}$ x

$\frac{4}{x}$

20．

如图，已知PB⊥AB，PC⊥AC，且PB=PC，D是AP上的一点，求证：BD=CD．

17．已知：b=

$\sqrt{21×22×23×24+1}$ -22²，试完成下列计算（1-

$\frac{a-b}{a+2b}$ ÷

$\frac{{a}^{2}-{b}^{2}}{{a}^{2}+4ab+4{b}^{2}}$ ）•（-

$\frac{a}{2{b}^{2}}$ -

$\frac{1}{2b}$ ）．

4．

在如图的9个方格内填入5个2和4个-2，使每行、每列、每条对角线上的三个数的乘积都是8．

14．已知：有理数m所表示的点到点2距离3个单位，a、b互为相反数，且都不为零，c、d互为倒数．
（1）求m的值；
（2）求代数式：2（a+b）+（

$\frac{a}{b}$ -3cd）-m的值．

1．已知⊙O的半径为5cm，P为⊙O外一点，则OP的长可能是（　　）

18．

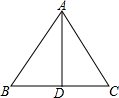如图，已知△ABC中，AB=AC，AD平分∠BAC，请补充完整过程说明△ABD≌△ACD的理由．
证明：∵AD平分∠BAC，
∴∠BAD=∠CAD（角平分线的定义）．
在△ABD和△ACD中，
∵AB=AC，∠BAD=∠CAD，AD=AD，
∴△ABD≌△ACDSAS．

19．单项式-

$\frac{2{π}^{2}{x}^{2}y}{3}$ 次数是3．

试题分类