题目内容
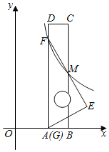
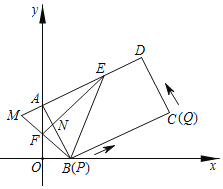
【题目】如图,在直角坐标系中,长方形ABCD(每个内角都是90°)的顶点的坐标分别是A(0,m),B(n,0),(m>n>0),点E在AD上,AE=AB,点F在y轴上,OF=OB,BF的延长线与DA的延长线交于点M,EF与AB交于点N.
(1)试求点E的坐标(用含m,n的式子表示);
(2)求证:AM=AN;
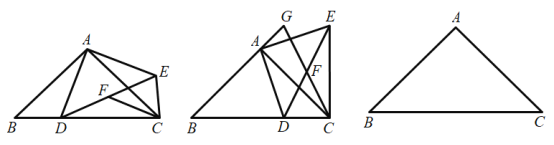
(3)若AB=CD=12cm,BC=20cm,动点P从B出发,以2cm/s的速度沿BC向C运动的同时,动点Q从C出发,以vcm/s的速度沿CD向D运动,是否存在这样的v值,使得△ABP与△PQC全等?若存在,请求出v值;若不存在,请说明理由.
【答案】(1)E(m,m+n);(2)详见解析;(3)存在,![]() cm/s或2cm/s.
cm/s或2cm/s.
【解析】
(1)过E作EG⊥AO于G.证明△EGA≌△AOB(AAS)即可解决问题.
(2)想办法证明△EAN≌△BAM(ASA)即可解决问题.
(3)分两种情形分别求解即可解决问题.
解:(1)过E作EG⊥AO于G.
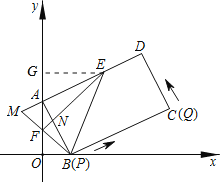
∵∠EGA=∠EAB=∠AOB=90°,
∴∠EAG+∠AEG=90°,∠EAG+∠BAO=90°,
∴∠BAO=∠AEG,
∵AE=AB,
∴△EGA≌△AOB(AAS),
∴EG=OA=m,AG=OB=n
∴E(m,m+n).
(2)∵OB=OF,∠BOF=90°,
∴∠OFB=∠OBF=45°,
∵△EGA≌△AOB,
∴AG=OB=OF,
∴OA=FG=EG,
∴∠GFE=45°,
∴∠EFB=90°,
∴∠NAE=∠NFB=90°,∵∠ANE=∠FNB,
∴∠AEN=∠ABM,
∵∠EAN=∠BAM=90°,EA=BA,
∴△EAN≌△BAM(ASA),
∴AN=AM.
(3)如图,∵△ABP与△PCQ全等,∠ABP=∠PCQ=90°

∴有两种情形:①当AB=CD,PB=CP时,t=![]() =5(s),
=5(s),
∴v=![]() (cm/s),
(cm/s),
②当AB=PC,CQ=PB时,
PB=20﹣12=8,
∴t=![]() =4(s),
=4(s),
∴v=![]() =
=![]() =2(cm/s).
=2(cm/s).
综上可知,当![]() cm/s或2 cm/s时,△ABP与△PQC全等.
cm/s或2 cm/s时,△ABP与△PQC全等.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案