题目内容
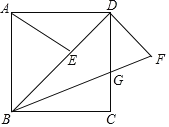
【题目】如图，矩形ABCD长与宽的比为3：2，点E，F分别在边AB、BC上，tan∠1＝
，tan∠2＝
，则cos（∠1+∠2）＝（ ）
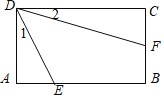
A.
B.
C.
D.1
【答案】B
【解析】
由“SAS”可证△AED≌△BFE，可得DE＝EF，∠1＝∠FEB，可证∠DEF＝90°，可求∠1+∠2＝45°，即可求解．
如图，连接EF
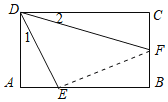
∵矩形ABCD长与宽的比为3：2
∴设AB＝CD＝3a，AD＝BC＝2a，
∵tan∠1=
∴AE=a，CF=a，
∴BF＝BC﹣CF＝a，BE＝AB﹣AE＝2a，
∴AE＝BF，AD＝EB，且∠A＝∠B＝90°
∴△AED≌△BFE（SAS）
∴DE＝EF，∠1＝∠FEB
∵∠1+∠DEA＝90°
∴∠DEA+∠FEB＝90°
∴∠DEF＝90°，且DE＝EF
∴∠EDF＝45°
∴∠1+∠2＝45°
∴cos（∠1+∠2）＝
故选：B．
练习册系列答案
优等生题库系列答案
相关题目
