题目内容
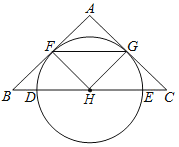
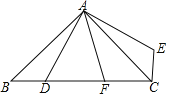
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D是BC上一动点,连接AD,过点A作AE⊥AD,并且始终保持AE=AD,连接CE.
(1)求证:△ABD≌△ACE;
(2)若AF平分∠DAE交BC于F,探究线段BD,DF,FC之间的数量关系,并证明;
(3)在(2)的条件下,若BD=3,CF=4,求AD的长.
【答案】(1)证明见解析;(2)结论:BD2+FC2=DF2.证明见解析;(3)![]() .
.
【解析】
(1)根据SAS,只要证明∠1=∠2即可解决问题;
(2)结论:BD2+FC2=DF2.连接FE,想办法证明∠ECF=90°,EF=DF,利用勾股定理即可解决问题;
(3)过点A作AG⊥BC于G,在Rt△ADG中,想办法求出AG、DG即可解决问题.
(1)证明:如图,
∵AE⊥AD,
∴∠DAE=∠DAC+∠2=90°,
又∵∠BAC=∠DAC+∠1=90°,
∴∠1=∠2,
在△ABD和△ACE中
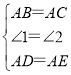 ,
,
∴△ABD≌△ACE.
(2)结论:BD2+FC2=DF2.理由如下:
连接FE,∵∠BAC=90°,AB=AC,
∴∠B=∠3=45°
由(1)知△ABD≌△ACE
∴∠4=∠B=45°,BD=CE
∴∠ECF=∠3+∠4=90°,
∴CE2+CF2=EF2,
∴BD2+FC2=EF2,
∵AF平分∠DAE,
∴∠DAF=∠EAF,
在△DAF和△EAF中
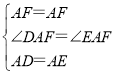 ,
,
∴△DAF≌△EAF
∴DF=EF
∴BD2+FC2=DF2.
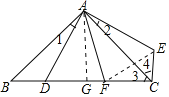
(3)过点A作AG⊥BC于G,
由(2)知DF2=BD2+FC2=32+42=25
∴DF=5,
∴BC=BD+DF+FC=3+5+4=12,
∵AB=AC,AG⊥BC,
∴BG=AG=![]() BC=6,
BC=6,
∴DG=BG-BD=6-3=3,
∴在Rt△ADG中,AD=![]() .
.

 阅读快车系列答案
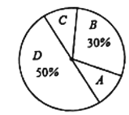
阅读快车系列答案【题目】研究机构对本地区18-20岁的大学生就某个问题做随机调查,要求被调查者从A、B、C、D四个选项中选择自己赞同的一项,并将结果绘制成两幅不完整的统计图(如图):
大学生就某个问题调查结果统计表 | 大学生就某个问题调查结果扇形统计图 | ||||||||||||
|
|
请结合图中信息解答以下问题:
(1)m=_____,b=_____.
(2)若该地区18~20岁的大学生有1.2万人,请估计这些大学生中选择赞同A选项的人数:
(3)该研究机构决定从选择“C”的人中随机抽取2名进行访谈,而选择“C”的这4人中只有一名男性,求这名男性刚好被抽取到的概率.
【题目】(7分)某中学1000名学生参加了”环保知识竞赛“,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)作为样本进行统计,并制作了如图频数分布表和频数分布直方图(不完整且局部污损,其中“■”表示被污损的数据).请解答下列问题:
成绩分组 | 频数 | 频率 |
50≤x<60 | 8 | 0.16 |
60≤x<70 | 12 | a |
70≤x<80 | ■ | 0.5 |
80≤x<90 | 3 | 0.06 |
90≤x≤100 | b | c |
合计 | ■ | 1 |
(1)写出a,b,c的值;
(2)请估计这1000名学生中有多少人的竞赛成绩不低于70分;
(3)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取两名同学参加环保知识宣传活动,求所抽取的2名同学来自同一组的概率.