题目内容
 如图所示,点C在线段BE上,在BE同侧作等边△ABC和等边△DCE,那么,从旋转的角度我们可以看到,△ACE旋转后与△BCD重合.
如图所示,点C在线段BE上,在BE同侧作等边△ABC和等边△DCE,那么,从旋转的角度我们可以看到,△ACE旋转后与△BCD重合.(1)写出旋转角的度数及旋转方向;
(2)在图中经过旋转后能够重合的三角形共有哪几对?
(3)如果∠2=40°,那么∠BDE=
80°
80°
.分析:(1)利用等边三角形的性质以及旋转的性质得出旋转角的度数及旋转方向;
(2)利用等边三角形的性质以及旋转的性质得出能够重合的三角形;
(3)利用旋转的性质以及等边三角形的性质得出∠BDE=∠BDC+∠CDE=20°+60°求出即可.
(2)利用等边三角形的性质以及旋转的性质得出能够重合的三角形;
(3)利用旋转的性质以及等边三角形的性质得出∠BDE=∠BDC+∠CDE=20°+60°求出即可.
解答:解:(1)从旋转的角度我们可以看到,△ACE逆时针旋转60°后与△BCD重合;
(2)能够重合的三角形有3对,分别为:△BCD和△ACE,△BCG和△ACF,△DCG和△EFC;
(3)∵△DCE是等边三角形,
∴∠DEC=∠CDE=60°,
∵∠2=40°,
∴∠AEC=20°,
∵△ACE旋转后与△BCD重合,
∴∠AEC=∠BDC=20°,
∴∠BDE=∠BDC+∠CDE=20°+60°=80°.
故答案为:80°.
(2)能够重合的三角形有3对,分别为:△BCD和△ACE,△BCG和△ACF,△DCG和△EFC;
(3)∵△DCE是等边三角形,
∴∠DEC=∠CDE=60°,
∵∠2=40°,
∴∠AEC=20°,
∵△ACE旋转后与△BCD重合,
∴∠AEC=∠BDC=20°,
∴∠BDE=∠BDC+∠CDE=20°+60°=80°.
故答案为:80°.
点评:此题主要考查了等边三角形的性质以及旋转的性质,注意利用旋转前后图形全等得出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 11、正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形ABCD的边长为4,FG=3,FP=1,则△DEK的面积为
11、正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形ABCD的边长为4,FG=3,FP=1,则△DEK的面积为 8、正方形ABCD,正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,且G为BC的三等分点,R为EF中点,正方形BEFG的边长为4,则△DEK的面积为( )
8、正方形ABCD,正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,且G为BC的三等分点,R为EF中点,正方形BEFG的边长为4,则△DEK的面积为( )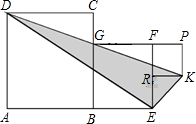 正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,已知正方形BEFG的边长为3,则△DEK的面积为
正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,已知正方形BEFG的边长为3,则△DEK的面积为 已知:如图所示,点C在线段AB上,分别以AC、BC为一边作为等边△ACM和等边△BCN,连接AN、BM.
已知:如图所示,点C在线段AB上,分别以AC、BC为一边作为等边△ACM和等边△BCN,连接AN、BM.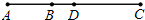 如图所示,点C在线段AB的延长线上,且BC=2AB,D是AC的中点,若AB=2cm,求BD的长.
如图所示,点C在线段AB的延长线上,且BC=2AB,D是AC的中点,若AB=2cm,求BD的长.