题目内容
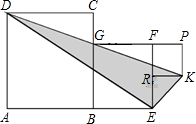正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示，点G在线段DK上，已知正方形BEFG的边长为3，则△DEK的面积为9
9
．分析：连BD、GE、FK，则DB∥GE∥FK，在梯形DBEG和梯形GEKF中，根据三角形的等积变换可得，S△GED=S△GEB，S△GEK=S△GEF，则可得S阴影=S正方形BEFG，再根据正方形BEFG的边长为3，解答出即可．运用平行线间的距离处处相等，同底等高来求面积，想起会更简便．
解答：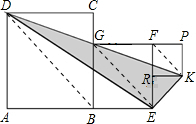
解：如图，连BD、GE、FK，则DB∥GE∥FK，
在梯形DBEG中，S△GED=S△GEB，
同理可得，S△GEK=S△GEF，
∴S阴影=S△GED+S△GEK，
=S△GEB+S△GEF，
=S正方形BEFG，
∵正方形BEFG的边长为3，
∴S阴影=3×3=9．
故答案为：9．
解：如图，连BD、GE、FK，则DB∥GE∥FK，在梯形DBEG中，S△GED=S△GEB，
同理可得，S△GEK=S△GEF，
∴S阴影=S△GED+S△GEK，
=S△GEB+S△GEF，
=S正方形BEFG，
∵正方形BEFG的边长为3，
∴S阴影=3×3=9．
故答案为：9．
点评：本题主要考查三角形的面积及等积变换，应用了正方形的性质、三角形及梯形的性质，体现了转化思想．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
（2013•常熟市模拟）如图，正方形ABCD中，点A、B的坐标分别为（0，10）（8，4），点C在第一象限，且CE⊥x轴于E点，动点P在正方形ABCD的边上，从A出发沿A-B-C-D以每秒1个单位的速度作匀速运动，同时点Q（1，0）以相同的速度在x轴上沿正方向运动，当P点到达D点时，两点同时停止，设运动时间为t秒．
如图，已知正方形ABCD的边长为4，将正方形置于平面直角坐标系xOy中，使AB在x轴的负半轴上，A点的坐标是（-1，0）．