题目内容
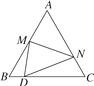
【题目】如图,在△ABC中,∠ACB=90°,BC=m,AB=3m,AC=n.
(1)将△ABC绕点B逆时针旋转,使点C落在AB边上的点C1处,点A落在点A1处,在图中画出△A1BC1;
(2)求四边形ACBA1的面积;(用m、n的代数式表示)
(3)将△A1BC1沿着AB翻折得△A2BC1,A2C1交AC于点D,写出四边形BCDC1与三角形ABC的面积的比值.

【答案】(1)画图见解析;(2)2mn;(3)![]() .
.
【解析】试题分析:(1)根据旋转的性质先A1点,然后连接A1B即可;(2)根据四边形ACBA1的面积= S△ABC+ S△ABA1求解即可;(3)根据S四边形BCDC1=S四边形ACBA1- S△ABA1求出四边形BCDC1面积,然后求比值.
解:如图,
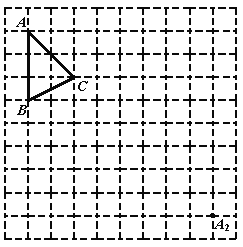
(1)画出△A1BC1;

(2)S△ABC= ![]() =
= ![]() ,
,
S△ABA1=![]() =
= ![]() ,
,
∴四边形ACBA1的面积是2mn;
(3)画出△A2BC1;
S四边形BCDC1=S四边形ACBA1- S△ABA1=2mn- ![]() =
= ![]() ,
,
∴四边形BCDC1与三角形ABC的面积的比值是![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目