题目内容
【题目】如图,已知直线l1∥l2,直线l3和直线l1,l2交于C、D两点,点P在直线CD上.
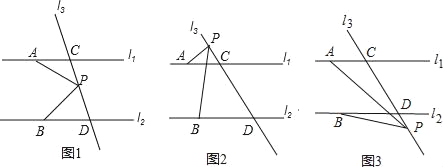
(1)试写出图1中∠APB、∠PAC、∠PBD之间的关系,并说明理由;
(2)如果P点在C、D之间运动时,∠APB、∠PAC、∠PBD之间的关系会发生变化吗?
答: (填发生或不发生)
(3)若点P在C、D两点的外侧运动时(P点与点C、D不重合),如图2,图3,试分別写出∠PAC、∠APB、∠PBD之间的关系,并说明理由.
【答案】见试题解析
【解析】
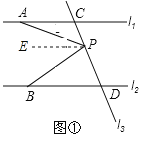
试题(1)过点P作PE∥l1,∠APE=∠PAC,又因为l1∥l2,所以PE∥l2,所以∠BPE=∠PBD,两个等式相加即可得出结论。(2)不发生(3)若点P在C、D两点的外侧运动时(P点与点C、D不重合),则有两种情形:①如图1,有结论:∠APB=∠PBD-∠PAC. 理由如下:
过点P作PE∥l1,则∠APE=∠PAC,又因为l1∥l2,所以PE∥l2,所以∠BPE=∠PBD,
所以可得出结论∠APB=∠PBD-∠PAC.。
②如图2,有结论:∠APB=∠PAC-∠PBD. 理由如下:过点P作PE∥l2,则∠BPE=∠PBD,
又因为l1∥l2,所以PE∥l1,所以∠APE=∠PAC,所以可得结论∠APB=∠PAC-∠PBD.
试题解析:解:(1)∠APB=∠PAC+∠PBD. 理由如下:
过点P作PE∥l1,
则∠APE=∠PAC,
又因为l1∥l2,所以PE∥l2,所以∠BPE=∠PBD,
所以∠APE+∠BPE=∠PAC+∠PBD,
即∠APB=∠PAC+∠PBD.
(2)若P点在C、D之间运动时∠APB=∠PAC+∠PBD这种关系不变.
(3)若点P在C、D两点的外侧运动时(P点与点C、D不重合),则有两种情形:
①如图1,有结论:∠APB=∠PBD-∠PAC. 理由如下:
过点P作PE∥l1,则∠APE=∠PAC,
又因为l1∥l2,所以PE∥l2,所以∠BPE=∠PBD,
所以∠APB=∠BPE-∠APE,即∠APB=∠PBD-∠PAC.
②如图2,有结论:∠APB=∠PAC-∠PBD. 理由如下:
过点P作PE∥l2,则∠BPE=∠PBD,
又因为l1∥l2,所以PE∥l1,所以∠APE=∠PAC,
所以∠APB=∠APE-∠BPE,即∠APB=∠PAC-∠PBD.
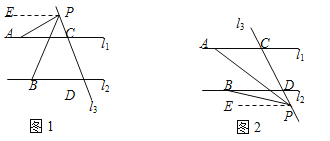

【题目】第二十四届冬季奥林匹克运动会将于2022年在北京市和张家口市举行.为了调查学生对冬奥知识的了解情况,从甲、乙两校各随机抽取20名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲校20名学生成绩的频数分布表和频数分布直方图如下:
甲校学生样本成绩频数分布表
成绩m(分) | 频数(人数) | 频率 |
| 1 | 0.05 |
| c | 0.10 |
| 3 | 0.15 |
| a | b |
| 6 | 0.30 |
合计 | 20 | 1.0 |
表1

图1
b.甲校成绩在![]() 的这一组的具体成绩是:81 81 89 83 89 82 83 89
的这一组的具体成绩是:81 81 89 83 89 82 83 89
c.甲、乙两校成绩的平均分、中位数、众数、方差如下:
学校 | 平均分 | 中位数 | 众数 | 方差 |
甲 | 84 | n | 89 | 129.7 |
乙 | 84.2 | 85 | 85 | 138.6 |
表2
根据以上图表提供的信息,解答下列问题:
(1)表1中a=______;表2中的中位数n =_______;
(2)补全图1甲校学生样本成绩频数分布直方图;
(3)在此次测试中,某学生的成绩是84分,在他所属学校排在前10名,由表中数据可知该学生是______校的学生(填“甲”或“乙”),理由是________;
(4)假设甲校1000名学生都参加此次测试,若成绩80分及以上为优秀,估计成绩优秀的学生人数为_______人.
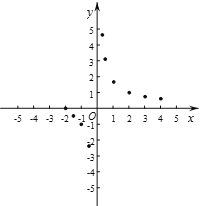
【题目】有这样一个问题:探究函数![]() 的图象与性质.小华根据学习函数的经验,对函数
的图象与性质.小华根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是___________;
的自变量x的取值范围是___________;
(2)下表是y与x的几组对应值.m的值为_______;
x | -2 |
| -1 |
|
|
| 1 | 2 | 3 | 4 | … |
y | 0 |
| m |
|
|
|
| 1 |
|
| … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)结合函数的图象,写出该函数的一条性质:____________.
(5)结合函数图象估计![]() 的解的个数为_______个.
的解的个数为_______个.