题目内容
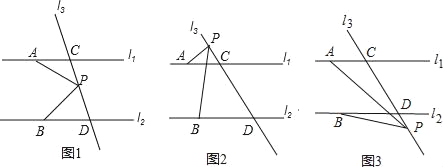
【题目】如图1 ，在矩形纸片
中，
，折叠纸片使
点落在边
上的
处，折痕为
，过点作
交于
，连接
求证：四边形
为菱形；
当点在边上移动时，折痕的端点
也随之移动，若限定分别在边
．上移动，求出点在边上移动的最大距离．
【答案】（1）见详解；（2）2．
【解析】
（1）根据折叠的性质得出
；再根据平行的性质及等角对等边得出
即可得证；
（2）根据正方形的性质，对称的性质以及勾股定理即可得出AE的值，从而得出DE的值；当点B与点M 重合时，点D离点E最近，此时DE=1cm，当点N与点C重合时，点D离点E最远，此时四边形EMCD为正方形，DE=DC=3cm，即可得出答案．
（1）
折叠纸片使
点落在边
上的
处，折痕为
，
点C与点E关于MN对称
四边形
为菱形；
（2）四边形ABCD为矩形
C、E关于MN对称
在
中，
当点B与点M 重合时，点D离点E最近，DE=1cm
当点N与点C重合时，点D离点E最远
此时四边形EMCD为正方形，DE=DC=3cm
点E在AD边上移动最大距离为2cm．
练习册系列答案
名校课堂系列答案
相关题目
【题目】某公司为了更好治理污水质，改善环境，决定购买10台污水处理设备，现有A，B两种型号的设备，其中每台的价格，月处理污水量如表：
A型 | B型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 200 | 160 |
经调查：购买一台A型设备比购买一台B型设备多3万元，购买2台A型设备比购买3台B型设备少1万元．
(1)求a，b的值；
(2)经预算：市治污公司购买污水处理设备的资金不超过78万元，你认为该公司有哪几种购买方案；
(3)在(2)间的条件下，若每月要求处理的污水量不低于1620吨，为了节约资金，请你为该公司设计一种最省钱的购买方案．
