��Ŀ����
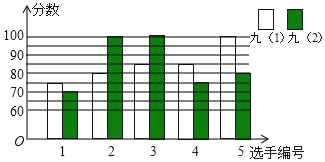
����Ŀ��Ϊѡ������ѡ�ֲμ��������ڰ˽�����Ļ������ڡ��о��䡱����������꼶��1������2������ݳ����ɼ�����ѡ��5��ѡ�ֲμӸ������������ѡ����5��ѡ�ֵĸ����ɼ���ͼ��ʾ
��1������ͼʾ��д�±�
�༶ | ƽ�������֣� | ��λ�����֣� | �������֣� |
�ţ�1�� | 85 | �� �� | 85 |
�ţ�2�� | �� �� | 80 | �� �� |
��2��������ิ���ɼ���ƽ��������λ���������ĸ��༶�ĸ����ɼ��Ϻã�
��3���������ิ���ɼ��ķ����˵���ĸ�������ѡ�ֵijɼ����ȶ���
���𰸡���1��
�༶ | ƽ�������֣� | ��λ�����֣� | �������֣� |
�ţ�1�� | 85 | 85 | 85 |
�ţ�2�� | 85 | 80 | 100 |
��2���ţ�1����ɼ���Щ��
��3���ţ�1��������ѡ�ֵijɼ����ȶ���
��������
��1���۲�ͼ�ֱ�д���ţ�1����;ţ�2����5��ѡ�ֵĸ����ɼ���Ȼ�������λ���Ķ����ƽ���������Լ������Ķ�����⼴�ɣ�
��2����ƽ������ͬ������£���λ���ߵijɼ��Ϻã�
��3�����ݷ��ʽ���㼴�ɣ�![]() ���ɼ���Ϊ�����ڲ��ƽ����������
���ɼ���Ϊ�����ڲ��ƽ����������
�⣺��1����ͼ��֪�ţ�1����5��ѡ�ֵĸ����ɼ�Ϊ��75��80��85��85��100��
��ţ�1������λ��Ϊ85��
�Ѿţ�2���ijɼ�����С�����˳������Ϊ��70��75��80��100��100��
��ţ�2����ƽ����Ϊ��70+75+80+100+100����5��85��
�ţ�2�����������100��
�༶ | ƽ�������֣� | ��λ�����֣� | �������֣� |
�ţ�1�� | 85 | 85 | 85 |
�ţ�2�� | 85 | 80 | 100 |
��2���ţ�1����ɼ���Щ����Ϊ�ţ�1�������λ���ߣ����Ծţ�1����ɼ���Щ��
��3��![]() [��75��85��2+��80��85��2+��85��85��2+��85��85��2+��100��85��2]��70��
[��75��85��2+��80��85��2+��85��85��2+��85��85��2+��100��85��2]��70��
![]() [��70��85��2+��100��85��2+��100��85��2+��75��85��2+��80��85��2]��160��
[��70��85��2+��100��85��2+��100��85��2+��75��85��2+��80��85��2]��160��
��![]() ��
��
��ţ�1��������ѡ�ֵijɼ����ȶ���