题目内容
【题目】若顺次连接四边形ABCD各边中点所得的四边形是矩形，则下列结论中正确的是（ ）
A.AB∥CDB.AB⊥BCC.AC=BDD.AC⊥BD
【答案】D
【解析】
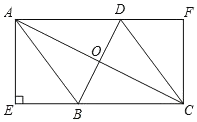
这个四边形ABCD的对角线AC和BD的关系是互相垂直．理由为：根据题意画出相应的图形，如图所示，由四边形EFGH为矩形，根据矩形的四个角为直角得到∠FEH=90°，又EF为三角形ABD的中位线，根据中位线定理得到EF与DB平行，根据两直线平行，同旁内角互补得到∠EMO=90°，同理根据三角形中位线定理得到EH与AC平行，再根据两直线平行，同旁内角互补得到∠AOD=90°，根据垂直定义得到AC与BD垂直．
如图：
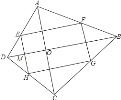
∵四边形EFGH是矩形，
∴∠FEH=90°，
又∵点E、F、分别是AD、AB、各边的中点，
∴EF是三角形ABD的中位线，
∴EF∥BD，
∴∠FEH=∠OMH=90°，
又∵点E、H分别是AD、CD各边的中点，
∴EH是三角形ACD的中位线，
∴EH∥AC，
∴∠OMH=∠COB=90°，
即AC⊥BD．
故选：D．
练习册系列答案
一本好题口算题卡系列答案
相关题目
【题目】下列数据是甲、乙、丙三人各10轮投篮的得分（每轮投篮10次，每次投中记1分）：
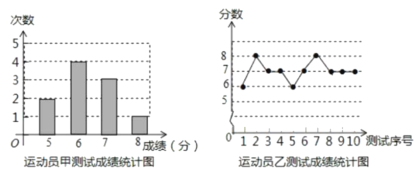
丙得分的平均数与众数都是7，得分统计表如下：
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
得分 | 7 | 6 | 8 | a | 7 | 5 | 8 | b | 8 | 7 |
（1）丙得分表中的a= ，b= ；
（2）若在他们三人中选择一位投篮得分高且较为稳定的投手作为主力，你认为选谁更合适？请用你所学过的统计知识加以分析说明（参考数据：
，
，
）；
（3）甲、乙、丙三人互相之间进行传球练习，每个人的球都等可能的传给其他两人，球最先从乙手中传出，经过三次传球后球又回到乙手中的概率是多少？（用树状图或列表法解答）
