题目内容
【题目】下列数据是甲、乙、丙三人各10轮投篮的得分(每轮投篮10次,每次投中记1分):
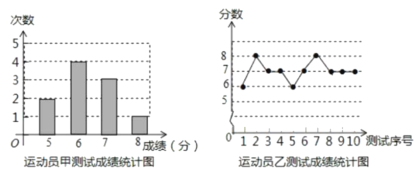
丙得分的平均数与众数都是7,得分统计表如下:
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
得分 | 7 | 6 | 8 | a | 7 | 5 | 8 | b | 8 | 7 |
(1)丙得分表中的a= ,b= ;
(2)若在他们三人中选择一位投篮得分高且较为稳定的投手作为主力,你认为选谁更合适?请用你所学过的统计知识加以分析说明(参考数据:![]() ,
,![]() ,
,![]() );
);
(3)甲、乙、丙三人互相之间进行传球练习,每个人的球都等可能的传给其他两人,球最先从乙手中传出,经过三次传球后球又回到乙手中的概率是多少?(用树状图或列表法解答)
【答案】(1)7,7;(2)选择乙更合适,理由是:在平均数相同的情况下,选择方差小的,因为方差越小,表示得分越稳定;(3)经过三次传球后球又回到乙手中的概率为![]() .
.
【解析】
(1)根据平均数的计算公式、众数的定义即可得;
(2)先计算出甲、乙的平均数,再利用平均数与方差的意义进行决策即可;
(3)先画出树状图,再找出事件的所有可能的结果,然后找出经过三次传球后球又回到乙手中的结果,最后利用概率公式计算即可得.
(1)![]() 丙得分的众数是7
丙得分的众数是7
![]() a和b中至少有一个等于7
a和b中至少有一个等于7
由平均数的公式得:![]()
整理得:![]()
则![]() ,
,![]()
故答案为:7,7;
(2)由图可知,甲10轮投篮的得分依次为![]()
乙10轮投篮的得分依次为![]()
则甲得分的平均数为![]()
乙得分的平均数为![]()
又因为![]() ,即
,即![]()
所以由平均数可知,应该选择乙、丙;由方差可知,选择乙更合适,理由是方差越小,表示得分越稳定
答:选择乙更合适,理由是:在平均数相同的情况下,选择方差小的,因为方差越小,表示得分越稳定;
(3)依题意,画树状图如下:

由此可知,经过三次传球的所有可能的结果共有8种,它们每一种出现的可能性都相等,其中,经过三次传球后球又回到乙手中的结果有2种
则所求的概率为![]()
答:经过三次传球后球又回到乙手中的概率为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某社区为了进一步提高居民珍惜谁、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每季度的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图和表:
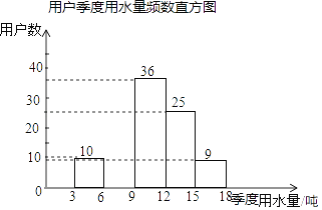
用户季度用水量频数分布表
平均用水量(吨) | 频数 | 频率 |
3<x≤6 | 10 | 0.1 |
6<x≤9 | m | 0.2 |
9<x≤12 | 36 | 0.36 |
12<x≤15 | 25 | n |
15<x≤18 | 9 | 0.09 |
请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m=_______,n=________;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本季度水量定为每户每季度9吨,不超过基本季度用水量的部分享受基本价格,超出基本季度用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?