题目内容
【题目】在![]() 是斜边
是斜边![]() 上的中线,将
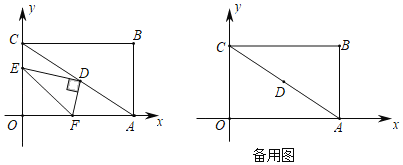
上的中线,将![]() 沿直线CM 折叠,点 A 落在点 D 处,如果CD 恰好与 AB 垂直,那么∠A 等于________度.
沿直线CM 折叠,点 A 落在点 D 处,如果CD 恰好与 AB 垂直,那么∠A 等于________度.
【答案】30
【解析】
先根据折叠的性质得∠1=∠2,由CM为直角△ABC斜边上的中线,根据直角三角形斜边上的中线性质得MA=MC=MB,则∠1=∠A,根据三角形外角性质得∠3=∠1+∠A=2∠1=2∠2,再由CD⊥AB得到∠3+∠2=90°,根据三角形内角和定理可计算出∠2=30°,即可得到结果.
解:如图,
∵△ABC的中线CM将△CMA折叠,使点A落在点D处,
∴∠1=∠2,
∵CM为直角△ABC斜边上的中线,
∴MA=MC=MB,
∴∠1=∠A,
∴∠2=∠A,∠3=∠1+∠A=2∠1=2∠2,
∵CD⊥AB,
∴∠3+∠2=90°,
∴2∠2+∠2=90°,
∴∠2=30°,
∴∠A=30°.
故答案为:30.


练习册系列答案
相关题目
【题目】某社区为了进一步提高居民珍惜谁、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每季度的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图和表:
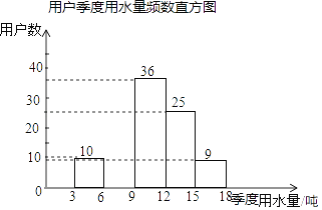
用户季度用水量频数分布表
平均用水量(吨) | 频数 | 频率 |
3<x≤6 | 10 | 0.1 |
6<x≤9 | m | 0.2 |
9<x≤12 | 36 | 0.36 |
12<x≤15 | 25 | n |
15<x≤18 | 9 | 0.09 |
请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m=_______,n=________;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本季度水量定为每户每季度9吨,不超过基本季度用水量的部分享受基本价格,超出基本季度用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?