Question

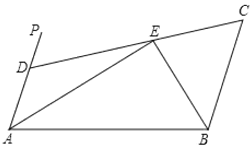
【题目】如图，，PAB的平分线与CBA的平分线相交于E，CE的延长线交AP于D，求证：

（1）AB=AD+BC；

（2）若BE=3，AE=4，求四边形ABCD的面积．

Answer 1

【答案】（1）证明见解析；（2）12．

【解析】

（1）此题要通过构造全等三角形来求解，延长AE交BC的延长线于M；由AP∥BC，及AE平分∠PAB，可求得∠BAE=∠M，即AB=BM，因此直线证得AD=MC即可；在等腰△ABM中，BE是顶角的平分线，根据等腰三角形三线合一的性质知：E是AM的中点，即AE=EM，而PA∥BM，即可证得△ADE≌△MCE，从而得到所求的结论．

（2）由（1）的全等三角形可知：△ADE、△MCE的面积相等，从而将所求四边形的面积转化为等腰△ABM的面积，易得AM、BE的值，从而根据三角形的面积公式求得△ABM的面积，即四边形ADCB的面积．

解：（1）延长AE交BC的延长线于M．

∵AE平分∠PAB，BE平分∠CBA，

∴∠1=∠2，∠3=∠4．

∵AD∥BC，

∴∠1=∠M=∠2，∠1+∠2+∠3+∠4=180°，

∴BM=BA，∠3+∠2=90°，

∴BE⊥AM．

在△ABE和△MBE中，

，

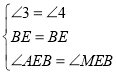∴△ABE≌△MBE，

∴AE=ME

在△ADE和△MCE中，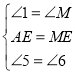

∴△ADE≌△MCE，

∴AD=CM，

∴AB=BM=BC+AD．

（2）由（1）知：△ADE≌△MCE，

∴S四边形ABCD=S△ABM

又∵AE=ME=4，BE=3，

∴，

∴S四边形ABCD=12．