题目内容
【题目】在△ABC中,∠B=90°,AB=BC,点D是BC边上的一点,连接AD,将AD绕点D顺时针旋转90°得到DE,作EF⊥BC交BC的延长线于点F.
(1)依题意补全图形;
(2)求证:EF=CF.
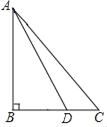
【答案】(1)如图所示见解析;(2)见解析.
【解析】
(1)依据AD绕点D顺时针旋转90°得到DE,作EF⊥BC交BC的延长线于点F进行作图.
(2)依据AAS判定△ABD≌△DFE,即可得到BD=EF,AB=DF,再根据AB=BC,可得BC=DF,进而得出BD=CF,等量代换可得EF=CF.
(1)如图所示:

(2)证明:由题可得,∠ADE=∠B=90°,AD=ED,
∴∠BAD+∠ADB=∠ADB+∠EDF=90°,
∴∠BAD=∠EDF,
在△ABD和△DFE中,
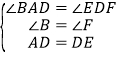 ,
,
∴△ABD≌△DFE(AAS),
∴BD=EF,AB=DF,
又∵AB=BC,
∴BC=DF,
∴BC﹣CD=DF﹣CD,即BD=CF,
∴EF=CF.

练习册系列答案
相关题目