题目内容
【题目】已知点A(a,m)在双曲线y=![]() 上且m<0,过点A作x轴的垂线,垂足为B.
上且m<0,过点A作x轴的垂线,垂足为B.
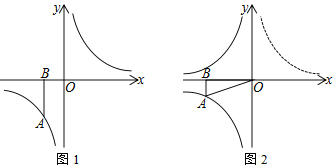
(1)如图1,当a=﹣2时,P(t,0)是x轴上的动点,将点B绕点P顺时针旋转90°至点C,
①若t=1,直接写出点C的坐标;
②若双曲线y=![]() 经过点C,求t的值.
经过点C,求t的值.
(2)如图2,将图1中的双曲线y=![]() (x>0)沿y轴折叠得到双曲线y=﹣
(x>0)沿y轴折叠得到双曲线y=﹣![]() (x<0),将线段OA绕点O旋转,点A刚好落在双曲线y=﹣
(x<0),将线段OA绕点O旋转,点A刚好落在双曲线y=﹣![]() (x<0)上的点D(d,n)处,求m和n的数量关系.
(x<0)上的点D(d,n)处,求m和n的数量关系.
【答案】(1)①C(1,3).②t=﹣4 或2;(2)满足条件的m、n的关系是m+n=0或mn=﹣8.
【解析】(1)①如图1﹣1中,求出PB、PC的长即可解决问题;
②图1﹣2中,由题意C(t,t+2),理由待定系数法,把问题转化为方程解决即可;
(2)分两种情形①当点A与点D关于x轴对称时,A(a,m),D(d,n),可得m+n=0.
②当点A绕点O旋转90°时,得到D′,D′在y=﹣![]() 上,作D′H⊥y轴,则△ABO≌△D′HO,推出OB=OH,AB=D′H,由A(a,m),推出D′(m,﹣a),即D′(m,n),由D′在y=﹣
上,作D′H⊥y轴,则△ABO≌△D′HO,推出OB=OH,AB=D′H,由A(a,m),推出D′(m,﹣a),即D′(m,n),由D′在y=﹣![]() 上,可得mn=﹣8.
上,可得mn=﹣8.
(1)①如图1﹣1中,

由题意:B(﹣2,0),P(1,0),PB=PC=3,
∴C(1,3);
②图1﹣2中,由题意C(t,t+2),

∵点C在y=![]() 上,
上,
∴t(t+2)=8,
∴t=﹣4 或2;
(2)如图2中,
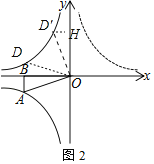
①当点A与点D关于x轴对称时,A(a,m),D(d,n),
∴m+n=0;
②当点A绕点O旋转90°时,得到D′,D′在y=﹣![]() 上,
上,
作D′H⊥y轴,则△ABO≌△D′HO,
∴OB=OH,AB=D′H,
∵A(a,m),
∴D′(m,﹣a),即D′(m,n),
∵D′在y=﹣![]() 上,
上,
∴mn=﹣8,
综上所述,满足条件的m、n的关系是m+n=0或mn=﹣8.

 阅读快车系列答案
阅读快车系列答案【题目】某市为了鼓励居民节约用水,采用分阶段计费的方法按月计算每户家庭的水费:月用水量不超过20m3时,按2元/m3计算;月用水量超过20m3时,其中的20m3仍按2元/m3计算,超过部分按2.6元/m3计算.设某户家庭月用水量xm3.
月份 | 4月 | 5月 | 6月 |
用水量 | 15 | 17 | 21 |
(1)用含x的式子表示:
当0≤x≤20时,水费为 元;
当x>20时,水费为 元.
(2)小花家第二季度用水情况如上表,小花家这个季度共缴纳水费多少元?