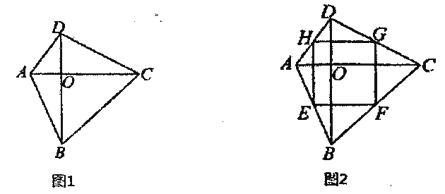题目内容
【题目】如图,已知抛物线![]() 的顶点C在x轴正半轴上,一次函数
的顶点C在x轴正半轴上,一次函数![]() 与抛物线交于A、B两点,与x、y轴交于D、E两点.
与抛物线交于A、B两点,与x、y轴交于D、E两点.

(1)求m的值.
(2)求A、B两点的坐标.
(3)点P(a,b)(![]() )是抛物线上一点,当△PAB的面积是△ABC面积的2倍时,求a,b的值.
)是抛物线上一点,当△PAB的面积是△ABC面积的2倍时,求a,b的值.
【答案】(1)3;(2)A(1,4),B(6,9);(3)![]() =
=![]() ,
,![]() =
=![]() .
.
【解析】
试题分析:(1)抛物线的顶点在x轴的正半轴上可知其对应的一元二次方程有两个相等的实数根,根据判别式等于0可求得m的值;
(2)由(1)可求得抛物线解析式,联立一次函数和抛物线解析式可求得A、B两点的坐标;
(3)分别过A、B、P三点作x轴的垂线,垂足分别为R、S、T,可先求得△ABC的面积,再利用a、b表示出△PAB的面积,根据面积之间的关系可得到a、b之间的关系,再结合P点在抛物线上,可得到关于a、b的两个方程,可求得a、b的值.
试题解析:(1)∵抛物线![]() 的顶点C在x轴正半轴上,∴方程
的顶点C在x轴正半轴上,∴方程![]() 有两个相等的实数根,∴
有两个相等的实数根,∴![]() ,解得m=3或m=﹣9,又抛物线对称轴大于0,即m+3>0,∴m=3;
,解得m=3或m=﹣9,又抛物线对称轴大于0,即m+3>0,∴m=3;
(2)由(1)可知抛物线解析式为![]() ,联立一次函数
,联立一次函数![]() ,可得
,可得 ,解得:
,解得:![]() 或
或![]() ,∴A(1,4),B(6,9);
,∴A(1,4),B(6,9);
(3)如图,分别过A、B、P三点作x轴的垂线,垂足分别为R、S、T,

∵A(1,4),B(6,9),C(3,0),P(a,b),∴AR=4,BS=9,RC=3﹣1=2,CS=6﹣3=3,RS=6﹣1=5,PT=b,RT=1﹣a,ST=6﹣a,∴S△ABC=S梯形ABSR﹣S△ARC﹣S△BCS=![]() ×(4+9)×5﹣
×(4+9)×5﹣![]() ×2×4﹣
×2×4﹣![]() ×3×9=15,S△PAB=S梯形PBST﹣S梯形ABSR﹣S梯形ARTP=
×3×9=15,S△PAB=S梯形PBST﹣S梯形ABSR﹣S梯形ARTP=![]() (9+b)(6﹣a)﹣
(9+b)(6﹣a)﹣![]() (b+4)(1﹣a)﹣
(b+4)(1﹣a)﹣![]() ×(4+9)×5=
×(4+9)×5=![]() (5b-5a﹣15),又S△PAB=2S△ABC,∴
(5b-5a﹣15),又S△PAB=2S△ABC,∴![]() (5b-5a﹣15)=30,即b-a=15,∴b=15+a,∵P点在抛物线上,∴
(5b-5a﹣15)=30,即b-a=15,∴b=15+a,∵P点在抛物线上,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,解得:
,解得:![]() ,∵
,∵![]() ,∴
,∴![]() =
=![]() ,∴
,∴![]() =
=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】《中国诗词大会》是央视首档全民参与的诗词节目,节目以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨,其中的一个比赛环节“飞花令”增加了节目悬念.新学期开学,某班组织了甲、乙两组同学进行了“飞花令”的对抗赛,规定说对一首得1分,比赛中有一方说出9首就结束两个人对抗,得6分以上为合格,得9分以上为优秀,甲、乙两组同学的一次测试成绩如下:
甲组:9,4,6,5,9,6,7,6,8,6,9,5,7,6,9
乙组:4,6,7,6,7,9,7,5,8,7,6,7,9,6,8
(1)请你根据所给的两组数据,绘制统计图(表).
(2)把下面的表格补充完整.
统计量 | 平均分(分) | 方差(分2) | 中位数(分) | 合格率 | 优秀率 |
甲组 | 2.56 | 6 | 80.0% | 26.7% | |
乙组 | 6.8 | 1.76 | 86.7% | 13.3% |
(3)根据第(2)题表中数据,你会支持哪一组,并说明理由.
【题目】探究题.
用棋子摆成的“T”字形图如图所示:

(1)填写表:
图形序号 | ① | ② | ③ | ④ | … | ⑩ |
每个图案中棋子个数 | 5 | 8 | … |
(2)写出第n个“T”字形图案中棋子的个数(用含n的代数式表示);
(3)第20个“T”字形图案共有棋子多少个?
(4)计算前20个“T”字形图案中棋子的总个数.(提示:请你先思考下列问题:第1个图案与第20个图案中共有多少个棋子?第2个图案与第19个图案中共有多少个棋子?第3个图案与第18个图案呢?)