题目内容
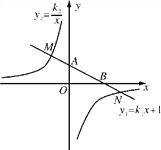
【题目】如图,在平面直角坐标系xOy中,一次函数y1=k1x+1的图象与y轴交于点A,与x轴交于点B,与反比例y2=![]() 象分别交于点M,N,已知△AOB的面积为1,点M的纵坐标为2.
象分别交于点M,N,已知△AOB的面积为1,点M的纵坐标为2.
(1)求一次函数与反比例函数的解析式;
(2)直接写出y1>y2时,x取值范围.
【答案】(1) y=-![]() x+1,y=-
x+1,y=-![]() ; (2) x<-2或0<x<4.
; (2) x<-2或0<x<4.
【解析】(1)先由一次函数的解析式为y1=k1x+1,求出点A与点B的坐标,再根据△AOB的面积为1,可得到k1的值,从而求出一次函数的解析式;进而得到点M的坐标,然后运用待定系数法即可求出反比例函数的解析式;
(2)y1>y2即一次函数值大于反比例函数值,只需观察一次函数的图象落在反比例函数的图象的上方时自变量的取值范围即可,为此,先求出它们的交点坐标,再根据函数图象,可知在点M的左边以及原点和点N之间的区间,y1>y2.
(1)∵一次函数y1=k1x+1的图象与y轴交于点A,与x轴交于点B,
∴A(0,1),B(﹣![]() ,0).
,0).
∵△AOB的面积为1,
∴![]() ×OB×OA=1,
×OB×OA=1,
![]() ×(﹣
×(﹣![]() )×1=1,
)×1=1,
∴k1=﹣![]() ,
,
∴一次函数的解析式为y1=﹣![]() x+1;
x+1;
当y=2时,﹣![]() x+1=2,解得x=﹣2,
x+1=2,解得x=﹣2,
∴M的坐标为(﹣2,2).
∵点M在反比例函数的图象上,
∴k2=﹣2×2=﹣4,
∴反比例函数的解析式为y2=﹣![]() ;
;
(2)解方程组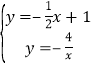 ,
,
得![]() 或
或![]() ,
,
故当y1>y2时,x<﹣2或0<x<4.

【题目】华联超市第一次用7000元购进甲、乙两种商品,其中甲商品的件数是乙商品件数的2倍,甲、乙两种商品的进价和售价如表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 20 | 30 |
售价(元/件) | 25 | 40 |
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍:甲商品按原价销售,乙商品打折销售,第二次两种商品都售完以后获得的总利润比第一次获得的总利润多800元,求第二次乙商品是按原价打几折销售?