题目内容
【题目】（1）化简：（
+1）÷
，并从﹣1、0、1、2这四个数中选取一个合适的数作为x的值代入求值．
（2）解方程： 
+2
【答案】（1）
，当x＝0时，原式＝﹣1；（2）方程无解
【解析】
（1）根据分式的加法和除法可以化简题目中的式子，然后从﹣1、0、1、2这四个数中选取一个使得原分式有意义的值代入化简后的式子即可解答本题；
（2）根据解分式方程的方法可以解答本题，注意分式方程要检验．
（1）（
+1）÷
＝
＝
＝，
∵x﹣2≠0，x﹣1≠0，
∴x≠2，x≠1，
当x＝0时，原式＝
＝﹣1；
（2）
＝
+2
方程两边同乘以3（x﹣3），得
2x+9＝3（4x﹣7）+2×3（x﹣3）
去括号，得
2x+9＝12x﹣21+6x﹣18
移项及合并同类项，得
﹣16x＝﹣48
系数化为1，得
x＝3，
经检验，x＝3不是原分式方程的根，
故原分式方程无解．
阅读快车系列答案【题目】甲、乙两校参加区教育局举办的学生英语口语竞赛，两校参赛人数相等.比赛结束后，发现学生成绩分别为7分、8分、9分、10分（满分为10分）.依据统计数据绘制了如图所示的尚不完整的统计图表.
甲校成绩统计表
分数 | 7分 | 8分 | 9分 | 10分 |
人数 | 11 | 0 | 8 |
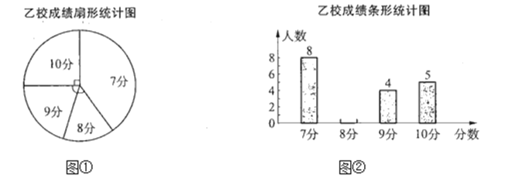
（1）在图①中，“7分”所在扇形的圆心角等于______
；
（2）请你将②的统计图补充完整；
（3）经计算，乙校的平均分是8.3分，中位数是8分，请写出甲校的平均分、中位数；并从平均分和中位数的角度分析哪个学校成绩较好；
（4）如果该教育局要组织8人的代表队参加市级团体赛，为便于管理，决定从这两所学校中的一所挑选参赛选手，请你分析，应选哪所学校？
【题目】某电器超市销售每台进价分别为200元，170元的A，B两种型号的电风扇，表中是近两周的销售情况：
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变，利润＝销售收入－进货成本)
(1)求A，B两种型号的电风扇的销售单价．
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台，则A种型号的电风扇最多能采购多少台？
(3)在(2)的条件下，超市销售完这30台电风扇能否实现利润为1400元的目标？若能，请给出相应的采购方案；若不能，请说明理由．
