题目内容
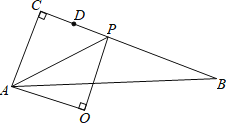
【题目】如图,Rt△ABC中,∠C=90°,AC=2,BC=5,点D是BC边上一点且CD=1,点P是线段DB上一动点,连接AP,以AP为斜边在AP的下方作等腰Rt△AOP.当P从点D出发运动至点B停止时,点O的运动路径长为_____.
【答案】2![]()
【解析】过O点作OE⊥CA于E,OF⊥BC于F,连接CO,如图,易得四边形OECF为矩形,由△AOP为等腰直角三角形得到OA=OP,∠AOP=90°,则可证明△OAE≌△OPF,所以AE=PF,OE=OF,根据角平分线的性质定理的逆定理得到CO平分∠ACP,从而可判断当P从点D出发运动至点B停止时,点O的运动路径为一条线段,接着证明CE=![]() (AC+CP),然后分别计算P点在D点和B点时OC的长,从而计算它们的差即可得到P从点D出发运动至点B停止时,点O的运动路径长.
(AC+CP),然后分别计算P点在D点和B点时OC的长,从而计算它们的差即可得到P从点D出发运动至点B停止时,点O的运动路径长.
过O点作OE⊥CA于E,OF⊥BC于F,连接CO,如图,

∵△AOP为等腰直角三角形,
∴OA=OP,∠AOP=90°,
易得四边形OECF为矩形,
∴∠EOF=90°,CE=CF,
∴∠AOE=∠POF,
∴△OAE≌△OPF,
∴AE=PF,OE=OF,
∴CO平分∠ACP,
∴当P从点D出发运动至点B停止时,点O的运动路径为一条线段,
∵AE=PF,
即AC-CE=CF-CP,
而CE=CF,
∴CE=![]() (AC+CP),
(AC+CP),
∴OC=![]() CE=
CE=![]() (AC+CP),
(AC+CP),
当AC=2,CP=CD=1时,OC=![]() ×(2+1)=
×(2+1)=![]() ,
,
当AC=2,CP=CB=5时,OC=![]() ×(2+5)=
×(2+5)=![]() ,
,
∴当P从点D出发运动至点B停止时,点O的运动路径长=![]() -
-![]() =2
=2![]() .
.
故答案为2![]() .
.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?