题目内容
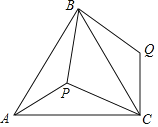
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC交于点D,DE⊥AC,垂足为E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)若∠C=60°,AC=12,求![]() 的长.
的长.
(3)若tanC=2,AE=8,求BF的长.
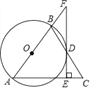
【答案】(1)见解析;(2) 2π;(3)![]() .
.
【解析】分析:(1)连接OD,根据等腰三角形的性质:等边对等角,得∠ABC=∠C,∠ABC=∠ODB,从而得到∠C=∠ODB ,根据同位角相等,两直线平行,得到OD∥AC,从而得证OD⊥EF,即 EF是⊙O的切线;
(2) 根据中点的性质,由AB=AC=12 ,求得OB=OD=![]() =6,进而根据等边三角形的判定得到△OBD是等边三角形,即∠BOD=600,从而根据弧长公式七届即可;
=6,进而根据等边三角形的判定得到△OBD是等边三角形,即∠BOD=600,从而根据弧长公式七届即可;
(3)连接AD ,根据直角三角形的性质,由在Rt△DEC中, ![]() 设CE=x,则DE=2x,然后由Rt△ADE中,
设CE=x,则DE=2x,然后由Rt△ADE中, ![]() ,求得DE、CE的长,然后根据相似三角形的判定与性质求解即可.
,求得DE、CE的长,然后根据相似三角形的判定与性质求解即可.
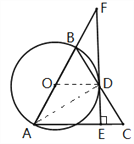
详解:(1)连接OD ∵AB=AC ∴∠ABC=∠C
∵OD=OB ∴∠ABC=∠ODB
∴∠C=∠ODB ∴OD∥AC
又∵DE⊥AC ∴OD⊥DE,即OD⊥EF
∴EF是⊙O的切线
(2) ∵AB=AC=12 ∴OB=OD=![]() =6
=6
由(1)得:∠C=∠ODB=600
∴△OBD是等边三角形 ∴∠BOD=600
∴![]() =
=![]() 即
即![]() 的长
的长![]()
(3)连接AD ∵DE⊥AC ∠DEC=∠DEA=900
在Rt△DEC中, ![]() 设CE=x,则DE=2x
设CE=x,则DE=2x
∵AB是直径 ∴∠ADB=∠ADC=900
∴∠ADE+∠CDE=900 在Rt△DEC中,∠C+∠CDE=900
∴∠C=∠ADE 在Rt△ADE中, ![]()
∵ AE=8,∴DE=4 则CE=2
∴AC=AE+CE=10 即直径AB=AC=10 则OD=OB=5
∵OD//AE ∴△ODF∽△AEF
∴ ![]() 即:
即:![]()
解得:BF=![]() 即BF的长为
即BF的长为![]() .
.