题目内容
【题目】某校在“筑梦少年正当时,不忘初心跟党走”知识竟赛中,七年级(2)班2人获一等奖,1人获二等奖,3人获三等奖,奖品价值41元;七年级(7)班1人获一等奖,3人获二等奖,3人获三等奖,奖品价值37元;七年级(13)班5人获二等奖,3人获三等奖,奖品价值_____元.
【答案】33
【解析】
设一等奖奖品的单价为x元/个,二等奖奖品的单价为y元/个,三等奖奖品的单价为z元/个,根据“2个一等奖、1个二等奖、3个三等将奖品价值41元;1个一等奖、3个二等奖、3个三等将奖品价值37元”,即可得出关于x、y、z的三元一次方程组,利用2×②﹣①即可求出结论.
设一等奖奖品的单价为x元/个,二等奖奖品的单价为y元/个,三等奖奖品的单价为z元/个,
根据题意得: ![]() ,
,
2×②﹣①,得:5y+3z=33.
故答案是:33.

练习册系列答案
相关题目
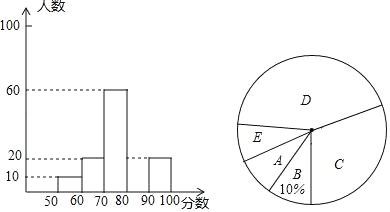
【题目】2018“体彩杯”重庆开州汉丰湖半程马拉松赛开跑前一周,某校七年级数学研究学习小组在某十字路口随机调查部分市民对“半马拉松赛”的了解情况,统计结果后绘制了如图的两副不完整的统计图,请结合图中相关数据回答下列问题:
A | 50<n≤60 |
B | 60<n≤70 |
C | 70<n≤80 |
D | 80<n≤90 |
E | 90<n≤100 |
(1)本次调查的总人数为 人,在扇形统计图中“C”所在扇形的圆心角的度数为 度;
(2)补全频数分布图;
(3)若在这一周里,该路口共有7000人通过,请估计得分超过80的大约有多少人?