题目内容
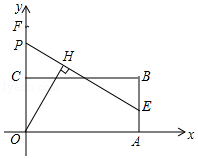
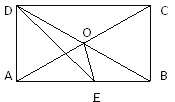
【题目】如图,在矩形ABCD中,DE平分∠ADC, 且∠EDO=15°,则∠OED=________°.
【答案】30
【解析】在矩形ABCD中,∠ADC=90°,DE平分∠ADC,则∠ADE=∠CDE=45°,
又∠EDO=15°,则∠ADO=∠ADE+∠EDO=60°,在矩形ABCD中,对角线AC与BD相等且互相平分,AO=DO,又∠ADO=60°,得△ADO是等边三角形,AO=DO=AD,
∠AOD=∠DAO=∠ADO=60°,又∠DAE=90°,∠ADE=45°,△ADE是等腰直角三角形,AD=AE,∠AED=∠ADE=45°,∴AO=AD=AE,△EAO是等腰三角形,∠AOE=∠AEO,
又∠EAO=90°-∠DAO=30°,得∠AEO=(180°-∠EAO)/2=75°,
∠OED=∠AEO-∠AED=75°-45°=30°,故答案为:30.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目