Question

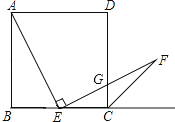
【题目】一块材料的形状是锐角三角形ABC，边BC=120mm，高AD=80mm，把它加工成正方形零件如图1，使正方形的一边在BC上，其余两个顶点分别在AB，AC上．

（1）求证：△AEF∽△ABC；
（2）求这个正方形零件的边长；
（3）如果把它加工成矩形零件如图2，问这个矩形的最大面积是多少？

Answer 1

【答案】
（1）

解：∵四边形EGFH为矩形，

∴BC∥EF，

∴△AEF∽△ABC；

（2）

解：设正方形零件的边长为amm

在正方形EFGH中，EF∥BC，EG∥AD

∴△AEF∽△ABC，△BFG∽△BAD

∴，，

∴，

即：

解得：a=48

即：正方形零件的边长为48mm；

（3）

设长方形的长为x，宽为y，

当长方形的长在BC时，

由1知：=1，

∵，

∴当，即x=60，y=40，xy最大为2400

当长方形的宽在BC时，，

∵，

∴当，即x=40，y=60，xy最大为2400，

又∵x≥y，所以长方形的宽在BC时，面积＜2400

综上，长方形的面积最大为2400mm2．

【解析】（1）根据矩形的对边平行得到BC∥EF，利用“平行于三角形的一边的直线截其他两边或其他两边的延长线，得到的三角形与原三角形相似”判定即可．
（2）根据正方形边的平行关系，得出对应的相似三角形，即△AEF∽△ABC，△BFG∽△BAD，从而得出边长之比 ， ，得到，进而求出正方形的边长；
（3）分别讨论长方形的长和宽在BC上的情况，再根据相应得关系式得出所求．
【考点精析】解答此题的关键在于理解相似三角形的应用的相关知识，掌握测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解．