Question

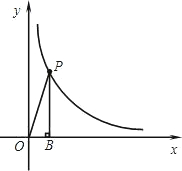
如图，在直角坐标系中，O为原点，A（4，12）为双曲线y=

k

x

（x＞0）上的一点．
（1）求k的值；
（2）过双曲线上的点P作PB⊥x轴于B，连接OP，若Rt△OPB两直角边的比值为

1

4

，试求点P的坐标；
（3）分别过双曲线上的两点P₁、P₂，作P₁B₁⊥x轴于B₁，P₂B₂⊥x轴于B₂，连接OP₁、OP₂．设Rt△OP₁B₁、Rt△OP₂B₂的周长分别为l₁、l₂，内切圆的半径分别为r₁、r₂，若

l1

l2

=2，试求

r1

r2

的值．

Answer 1

（1）将A（4，12）代入双曲线y=

k

x

中，得12=

k

4

，则k=48；（3分）

（2）由（1）得双曲线解析式为y=

48

x

，（4分）
设P（m，n），∴n=

48

m

，即mn=48，（5分）
当

OB

PB

=

1

4

时，即

m

n

=

1

4

，可设m=z，n=4z，
∴z•4z=48，解得z=2

3

，
∴m=2

3

，n=8

3

，
∴P（2

3

，8

3

），（7分）
当

PB

OB

=

1

4

时，同理可求得P（8

3

，2

3

）；（8分）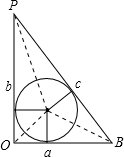

（3）在Rt△OP₁B₁中，设OB₁=a₁，P₁B₁=b₁，OP₁=c₁，
则P₁（a₁，b₁），由（2）得a₁b₁=48，
在Rt△OP₂B₂中，设OB₂=a₂，P₂B₂=b₂，OP₂=c₂，
则P₂（a₂，b₂），由（2）得a₂b₂=48，
∵

1

2

(a1+b1+c1)•r1=

1

2

a1b1=24

1

2

(a2+b2+c2)•r2=

1

2

a2b2=24（10分）
∴（a₁+b₁+c₁）•r₁=（a₂+b₂+c₂）•r₂（11分）
即l₁•r₁=l₂•r₂，故

l1

l2

=

r2

r1

（12分）
又∵

l1

l2

=2，∴

r2

r1

=2，即得：

r1

r2

=

1

2

．（13分）