题目内容
【题目】如图,在△ABC中,AB=AC,∠A=120°,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,若MN=2,则NF=___________

【答案】1
【解析】
连接AN、AM,根据等腰三角形性质可知∠B=∠C=30°,利用线段垂直平分线定理可得BM=AM,AN=CN,根据等边对等角可知∠B=∠MAB,∠NAC=∠C,即可知道△AMN是等边三角形,进而得到AN的长,利用直角三角形中30°角所对的直角边是斜边的一半,即可求得NF的长.
如图,连接AN、AM,
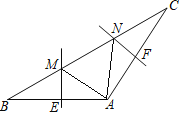
∵AB=AC,∠A=120°,
∴∠B=∠C=30°,
∵ME、NF分别垂直平分线段AB、AC
∴BM=AM,AN=CN,
∴∠B=∠MAB=30°,∠NAC=∠C=30°,
∴∠AMN=∠MAN=∠MNA=60°
∴△AMN是等边三角形,
∴AN=MN=2
在Rt△ANF中,∠NAF=30°
∴NF=![]() AN=1
AN=1
故答案为:1

练习册系列答案
相关题目