题目内容
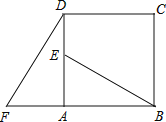
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,四边形
,四边形![]() 为平行四边形,
为平行四边形,![]() 在
在![]() 轴上一定点,
轴上一定点,![]() 为
为![]() 轴上一动点,且点
轴上一动点,且点![]() 从原点
从原点![]() 出发,沿着
出发,沿着![]() 轴正半轴方向以每秒
轴正半轴方向以每秒![]() 个单位长度运动,已知
个单位长度运动,已知![]() 点运动时间为
点运动时间为![]() .
.
(1)点![]() 坐标为________,
坐标为________,![]() 点坐标为________;(直接写出结果,可用
点坐标为________;(直接写出结果,可用![]() 表示)
表示)
(2)当![]() 为何值时,
为何值时,![]() 为等腰三角形;
为等腰三角形;
(3)![]() 点在运动过程中,是否存在
点在运动过程中,是否存在![]() ,使得
,使得![]() ,若存在,请求出
,若存在,请求出![]() 的值,若不存在,请说明理由!
的值,若不存在,请说明理由!

【答案】(1)(4,4),(![]() ,0);(2)1,
,0);(2)1,![]() ,4; (3)存在,
,4; (3)存在,![]()
【解析】
(1)利用平行四边形的性质和根据P点的运动速度,利用路程公式求解即可;
(2)分三种情况:①当![]() 时,②当
时,②当![]() 时,③当
时,③当![]() 时,分别讨论求解,即可得出结果;
时,分别讨论求解,即可得出结果;
(3)过D点作![]() 交BP于点F,设
交BP于点F,设![]() ,则可得
,则可得![]() ,
,![]() ,
,![]() ,利用
,利用![]() ,即可求出
,即可求出![]() 的长,利用路程公式可求得
的长,利用路程公式可求得![]() 的值。
的值。
解:(1)∵![]() ,
,![]() ,四边形
,四边形![]() 为平行四边形,
为平行四边形,
∴点![]() 坐标为(4,4),
坐标为(4,4),
又∵![]() 为
为![]() 轴上一动点,点
轴上一动点,点![]() 从原点
从原点![]() 出发,沿着
出发,沿着![]() 轴正半轴方向以每秒
轴正半轴方向以每秒![]() 个单位长度运动,
个单位长度运动,![]() 点运动时间为
点运动时间为![]() ,
,
∴![]() 点坐标为(
点坐标为(![]() ,0),
,0),
(2)∵B,D的坐标分别为:![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
由勾股定理有:![]() ,
,
当![]() 为等腰三角形时,
为等腰三角形时,
①如图所示,当![]() 时,
时,
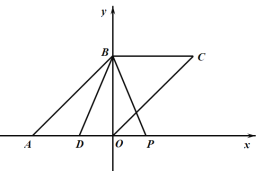
![]() ,
,
∴![]() 点坐标为(
点坐标为(![]() ,0),
,0),
∴![]()
②如图所示,当![]() 时,
时,
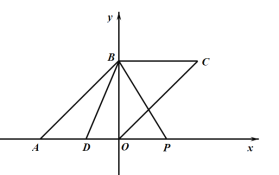
∵![]() ,
,![]()
∴![]() ,
,
∴![]()
③如图所示,当![]() 时,
时,

设P点坐标为:(![]() ,0)
,0)
则有:![]() ,
,![]() ,
,
∴![]() ,解之得:
,解之得:![]()
∴![]() 点坐标为(
点坐标为(![]() ,0),
,0),
∴![]()
综上所述,当![]() 为1,
为1,![]() ,4时,
,4时,![]() 为等腰三角形;
为等腰三角形;
(3)答:存在![]() ,使得
,使得![]() 。
。
证明:∵A,B两点坐标分别为:![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]()
∴![]()
即有:![]() ,
,
如图示,过D点作![]() 交BP于点F,
交BP于点F,

∵![]() ,
,
∴![]() ,
,
设![]() ,根据勾股定理有:
,根据勾股定理有:![]() ,
,
并且![]() ,
,
则:![]()
∴![]() ,
,
化简得:![]() ,
,
解之得:![]() (取正值),
(取正值),
即![]()
∴![]() .
.

练习册系列答案
相关题目