Question

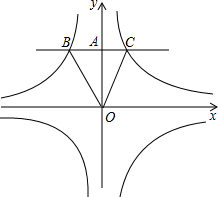如图，已知反比例函数y=

k1

x

（k₁＞0）和y=

k2

x

（k₂＜0），点A在y轴的正半轴上，过点A作直线BC∥x轴，且分别与两个反比例函数的图象交于点B和C，连接OC、OB．若△BOC的面积为

5

2

，AC：AB=2：3，则k₁•k₂=

-6

．

Answer 1

分析：根据反比例函数y=

k

x

（k≠0）系数k的几何意义得到S_△ABO=-

1

2

k₁，S_△ACO=

1

2

k₂，而△BOC的面积为

5

2

，AC：AB=2：3，根据三角形面积公式得到S_△ABO=

3

5

S_△BOC=

3

2

，S_△ACO=

2

5

S_△BOC=1，即有-

1

2

k₁=

3

2

，

1

2

k₂=1，然后计算出k₁，k₂，最后计算它们的乘积．

解答：解：∵BC∥x轴，
∴S_△ABO=

1

2

|k₁|=-

1

2

k₁，S_△ACO=

1

2

|k₂|=

1

2

k₂，
∵△BOC的面积为

5

2

，AC：AB=2：3，
∴S_△ABO=

3

5

S_△BOC=

3

5

×

5

2

=

3

2

，S_△ACO=

2

5

S_△BOC=

2

5

×

5

2

=1，
∴-

1

2

k₁=

3

2

，

1

2

k₂=1，
∴k₁=-3，k₂=2，
∴k₁•k₂=-3×2=-6．
故答案为-6．

点评：本题考查了反比例函数y=

k

x

（k≠0）系数k的几何意义：从反比例函数y=kx（k≠0）图象上任意一点向x轴和y轴作垂线，垂线与坐标轴所围成的矩形面积为|k|．