题目内容
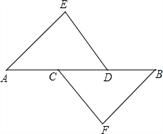
【题目】已知:如图,AE∥BF,∠E=∠F,DE=CF,
(1)求证:AC=BD;
(2)请你探索线段DE与CF的位置关系,并证明你的结论.
【答案】(1)见解析 (2)见解析
【解析】试题分析:(1)先根据两直线平行,内错角相等证得∠A=∠B,再根据∠A=∠B,∠E=∠F,DE=CF可证得△AED≌△BFC,再根据全等三角形的性质可得AD=BC,根据线段和差关系得:AC=BD,
(2) 因为(1)中△AED≌△BFC,所以∠EDA=∠FCB,根据内错角相等,两直线平行,
可证DE∥CF.
(1)∵AE∥BF, ∴∠A=∠B,
在△ADE和△BCF中,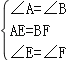 ,
,
∴△ADE≌△BCF,∴AD=BC,
∴AD﹣DC=BC﹣CD,
即:AC=BD .
(2)DE∥CF.
∵△ADE≌△BCF,
∴∠ADE=∠BCF,
∴DE∥CF.

练习册系列答案
相关题目