题目内容
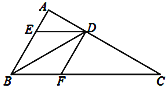
【题目】如图,AB为⊙O的直径,点C、点D为⊙O上异于A、B的两点,连接CD,过点C作CE⊥DB,交DB的延长线于点E,连接AC、AD、BC,若∠ABD=2∠BDC.
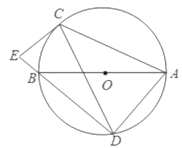
(1)求证:CE是⊙0的切线
(2)求证:△ABC![]() △CBE
△CBE
(3)若⊙O的半径为5,tan∠BDC=![]() ,求BE的长.
,求BE的长.
【答案】(1)见解析;(2)见解析;(3)2
【解析】
(1)连接OC,可证明OC∥DE,由于CE⊥DB,∠CED=90°,所以∠OCE=90°,OC⊥CE,根据切线的判定即可求出答案;
(2)由AB是⊙O的直径,可得![]() ,可得
,可得![]() ,再证∠ECB=∠CAB,即可得出结论;
,再证∠ECB=∠CAB,即可得出结论;
(3)连接BC,由于∠BDC=∠BAC,所以![]() ,设BC=x,AC=2x,所以
,设BC=x,AC=2x,所以![]() ,列出方程即可求出x的值,利用△ABC
,列出方程即可求出x的值,利用△ABC![]() △CBE可求出BE的长度.
△CBE可求出BE的长度.
(1)证明:连接![]()

∵![]()
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∵![]() ,
,
∴![]()
∴![]() ,
,
∴![]()
∵OC为![]() 的半径
的半径
∴![]() 是
是![]() 的切线
的切线
(2)连接![]()

∵AB是⊙O的直径
∴![]()
∴![]()
∵∠ECO=∠BCA=90°
∴∠ECB+∠BCO=∠OCA+∠BCO
∴∠ECB=∠OCA
∵![]()
∴∠ECB=∠CAB
∴△ABC![]() △CBE
△CBE
(3)∵![]() ,
,
∴![]()
∵![]() 是
是![]() 的直径
的直径
∴![]()
∴![]()
设![]() ,
,![]()
∴![]()
∵![]() 的半径为5
的半径为5
∴![]()
∴![]()
∴![]()
∵△ABC![]() △CBE
△CBE
∴![]()
∴![]()
∴BE=2

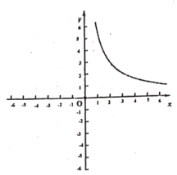
【题目】某班数学兴趣小组对函数![]() 的图象和性质将进行了探究,探究过程如下,请补充完整.
的图象和性质将进行了探究,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是除0外的全体实数,
的取值范围是除0外的全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
| … |
|
|
|
| 1 | 2 | 3 | 6 | … |
| … | 1 | 2 |
| 6 | 1 | 3 | 2 | 1 | … |
其中,![]() _________.
_________.
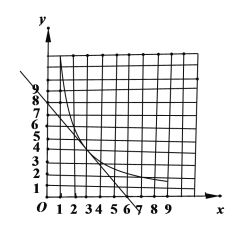
(2)根据上表数据,在如图所示的平面直角坐标系中描点并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出一条函数性质.
(4)进一步探究函数图象发现:
①函数图象与![]() 轴交点情况是________,所以对应方程
轴交点情况是________,所以对应方程![]() 的实数根的情况是________.
的实数根的情况是________.
②方程![]() 有_______个实效根;
有_______个实效根;
③关于![]() 的方程
的方程![]() 有2个实数根,
有2个实数根,![]() 的取值范围是________.
的取值范围是________.