Question

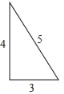
【题目】已知等腰三角形ABC的底边长BC=20cm，D是AC上的一点，且BD=16cm，CD=12cm．

（1）求证：BD⊥AC；

（2）求△ABC的面积．

Answer 1

【答案】（1）见解析；（2）△ABC的面积为cm2．

【解析】

（1）根据勾股定理的逆定理证明即可

（2）根据勾股定理先求出BD，然后再求三角形的面积即可

（1）∵BC=20，BD=16，CD=12

122+162=202

∴CD2+BD2=BC2，

∴△BDC是直角三角形，

∴BD⊥AC；

（2）解：设AD=xcm，则AC=（x+12 ）cm，

∵AB=AC，

∴AB═（x+12 ）cm，

在Rt△ABD中：AB2=AD2+BD2，

∴（x+12）2=162+x2，

解得x=，

∴AC= +12=cm，

∴△ABC的面积S=BDAC=×16×=cm2．