��Ŀ����
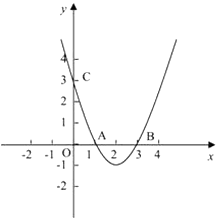
����Ŀ����ͼ��������y=ax2+bx+c��a��0����y�ύ�ڵ�C��0��4������x�ύ�ڵ�A�͵�B�����е�A������Ϊ����2��0���������ߵĶԳ���x=1�������߽��ڵ�D����ֱ��BC���ڵ�E��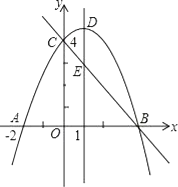
��1���������ߵĽ���ʽ��
��2����ֱ��BC�ĺ�������ʽΪy��=kx+b,������y<y��ʱ���Ա���x��ȡֵ��Χ.
��3��ƽ����DE��һ����ֱ��l��ֱ��BC�ཻ�ڵ�P�����������ཻ�ڵ�Q������D��E��P��QΪ������ı�����ƽ���ı��Σ����P�����꣮
���𰸡�
��1���⣺��������y=ax2+bx+c��a��0������C��0��4����
��c=4 �٣�
�߶Գ���x=- ![]() =1��
=1��
��b=-2a �ڣ�
�������߹���A��-2��0����
��0=4a-2b+c �ۣ�
�ɢ٢ڢ۽�ã�a=- ![]() ��b=1��c=4��
��b=1��c=4��
�������ߵĽ���ʽΪy=- ![]() x2+x+4��
x2+x+4��
��2���⣺��A����2��0�����Գ���x=1��
��B��4��0��
����ͼ��x<0 ��x>4ʱ��y
��3���⣺��֪DE��PQ����DE=PQʱ����D��E��P��QΪ������ı�����ƽ���ı��Σ�
���P�������ǣ�m����m+4�������Q�������ǣ�m���� ![]() m2+m+4����
m2+m+4����
��|��m+4+ ![]() m2��m��4|=DE=
m2��m��4|=DE= ![]() ��
��

��m=1��m=3��m= ![]() ��m=
��m= ![]()
��m=1ʱ���߶�PQ��DE�غϣ���ȥ��
��P1��3��1����
P2�� ![]() ��
�� ![]() ����
����
P3�� ![]() ��
�� ![]() ��.
��.
����������1������һ�����ݵ�C����������c=4�����ݶԳ���x=1���ó�b=-2a ������A������������ʽ�ó�0=4a-2b+c ��������⣬���������������ʽ�������������ݶ��κ����ĶԳ��ԣ��ɵ�A�����꼰�����ߵĶԳ���x=1�������B�����꣬Ȼ���躯������ʽΪ����ʽ���ٽ���C������������a��ֵ�����������������ʽ��
��2���������B�����꣬���ݵ�A��B�����꣬�۲캯��ͼ��Ҫʹy<y��ʱ����Ҫ�۲������ߵ���ֱ��BC�IJ��֣�������������
��3��ץס��֪����ƽ����DE��һ����ֱ��l����֪DE��PQ����P�͵�Q�ĺ�������ȣ�Ҫ֤��D��E��P��QΪ������ı�����ƽ���ı��Σ�ֻ��֤��DE=PQ���ɡ��ȸ��ݵ�P�͵�Q�ĺ�������ȣ��ֱ�����������꣬�ٸ���DE=PQ�������̣���⼴����õ�P�����ꡣ
�����㾫����ͨ���������ƽ���ı��ε��ж������ʣ�������һֱ�߹�ƽ���ı������Խ��ߵĽ��㣬������ֱ�߱�һ��Ա߽��µ��߶��ԶԽ��ߵĽ���Ϊ�е㣬����������ֱ�߶��ȷִ�ƽ���ı��ε���������Խ����⣮

 ����˼ά�żӿ���ϵ�д�
����˼ά�żӿ���ϵ�д� �����Ծ�ϵ�д�
�����Ծ�ϵ�д�