题目内容
(本题满分12分)
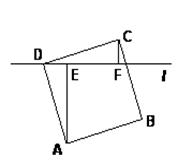
已知:如图,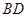 为平行四边形ABCD的对角线,
为平行四边形ABCD的对角线,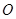 为
为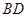 的中点,
的中点,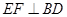 于点
于点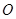 ,与
,与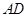 ,
,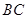 分别交于点
分别交于点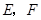 .
.

求证:⑴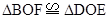 .
.
⑵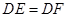
已知:如图,
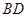 为平行四边形ABCD的对角线,
为平行四边形ABCD的对角线,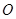 为
为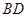 的中点,
的中点,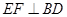 于点
于点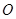 ,与
,与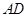 ,
,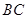 分别交于点
分别交于点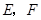 .
.
求证:⑴
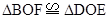 .
.⑵
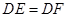
(1)∵四边形ABCD是平行四边形
∴AD∥BC
∴∠OED=∠OFB ∠EDO=∠FBO
又∵OB=OD
∴△BOF≌△DOE
(2)、∵△BOF≌△DOE∴OE=OF
∵BD⊥EF,∴DE=DF
∴AD∥BC
∴∠OED=∠OFB ∠EDO=∠FBO
又∵OB=OD
∴△BOF≌△DOE
(2)、∵△BOF≌△DOE∴OE=OF
∵BD⊥EF,∴DE=DF
试题分析:证明:(1)∵四边形ABCD是平行四边形
∴AD∥BC
∴∠OED=∠OFB ∠EDO=∠FBO
又∵OB=OD
∴△BOF≌△DOE
(2)、∵△BOF≌△DOE∴OE=OF
∵BD⊥EF,∴DE=DF
点评:本题难度较低。运用全等三角形的判定性质证明即可。

练习册系列答案
相关题目
 中,
中,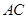 、
、 相交于点
相交于点 ,已知
,已知 ,
, = (度).
= (度).
 cm,则另一条对角线的长( )
cm,则另一条对角线的长( )
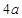 ,CF=
,CF=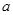 ,则正方形ABCD的面积为 .
,则正方形ABCD的面积为 .